Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Les mathématiques

du sofa

  • 15 minutes de lecture
Picture of Christian Genest

Christian Genest

professeur de statistique (Université McGill)

Picture of Christiane Rousseau

Christiane Rousseau

professeure émérite de mathématiques (Université de Montréal)

Un sofa doit être déplacé le long d’un corridor en L. Si on souhaite que le sofa soit le plus grand possible et qu’il puisse passer le coin sans être soulevé, quelle forme doit-il avoir ? Ce problème, posé en 1966 par le mathématicien austro-canadien Leo Moser, a fait l’objet de plusieurs publications scientifiques. Il se prête bien à une exploration dans le cadre d’un atelier de résolution de problèmes ou d’un projet de fin d’études.

Nous allons proposer ici quelques pistes de solution à explorer avec des élèves du niveau secondaire. Avant de les faire réfléchir sur les exemples discutés dans l’article, il nous semble judicieux de les inviter à dessiner le corridor sur une feuille de papier et à découper des sofas de différentes formes qu’ils pourront essayer de faire glisser dans le corridor. Pour simplifier les choses, on peut supposer que celui-ci a 1 mètre de largeur et que le sofa doit être déplacé de gauche à droite, comme dans la figure 1.


Figure 1. Déplacement d’un sofa carré le long d’un corridor en L

Dans cette figure, on constate qu’un sofa carré de côté 1 peut aisément passer le coin. Pour cela, on le translate horizontalement, puis verticalement. Donc, l’aire du plus grand sofa possible est au moins égale à 1. Pour stimuler les élèves, on peut leur révéler d’entrée de jeu que l’aire maximale du sofa est d’environ 2,2195 m2, comme un jeune mathématicien coréen du nom de Jineon Baek l’a annoncé en décembre 2024.

1re exploration : le sofa rectangulaire

Peut-on faire mieux avec un rectangle de largeur l < 1 et de longueur L > l ? En effet, au contraire d’un sofa carré, un sofa rectangulaire pourrait peut-être tourner le coin, tel qu’illustré à la figure 2.

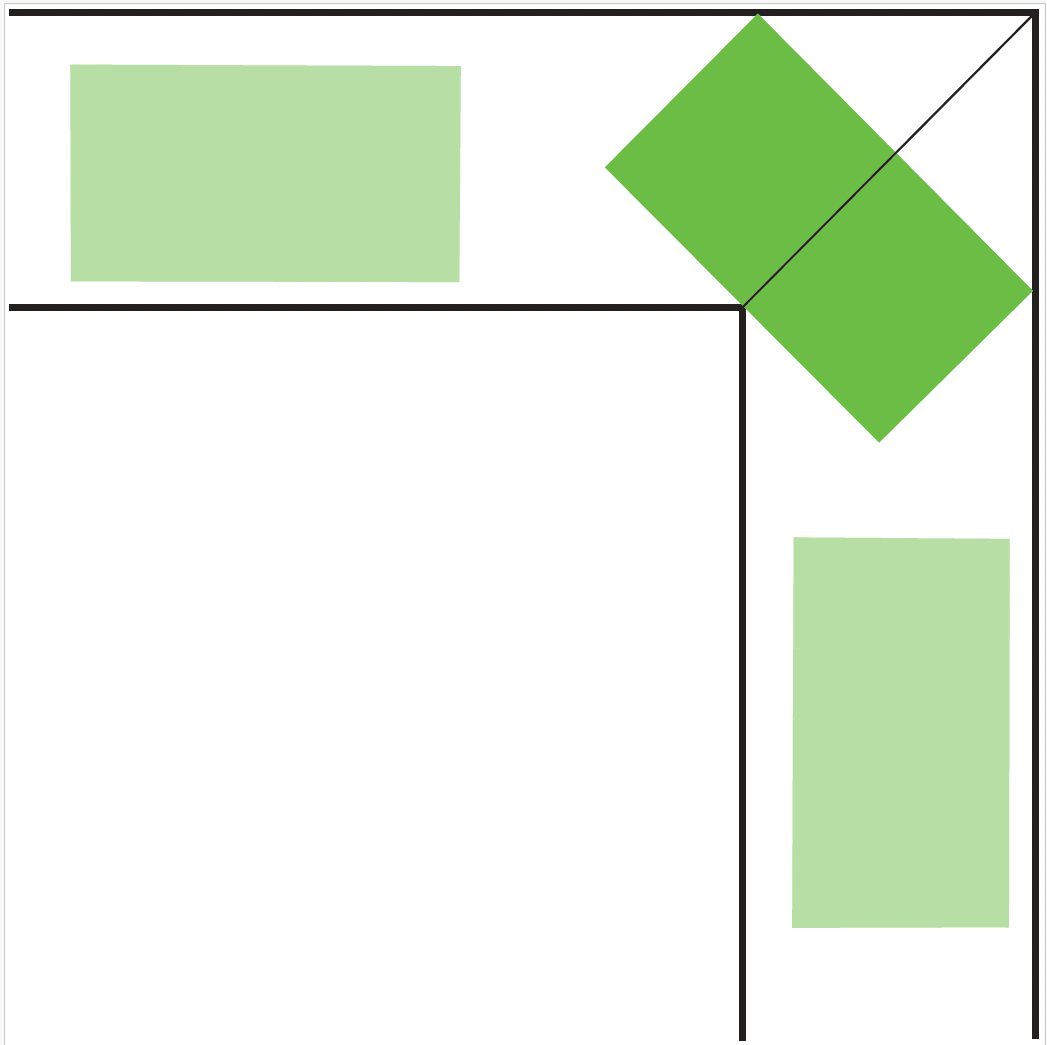
Figure 2. Déplacement d’un sofa rectangulaire le long d’un corridor en L

On peut se convaincre sans peine que la position critique se produit quand le sofa fait un angle de 45o avec les parties horizontale et verticale du corridor. Pour cela, on peut expérimenter en jouant avec des sofas en carton que l’on fait tourner sur un corridor dessiné sur une feuille de papier1. Pour qu’un sofa d’aire maximale passe le coin, il faut qu’au moment où il est tourné à 45o, deux de ses coins touchent les murs intérieurs et que le côté opposé touche le coin intérieur du corridor, comme on peut le voir sur la figure 3. Quelles sont alors les dimensions du sofa ? D’une part, la longueur de la diagonale du coin est \( \sqrt{2} \).  Quand on se réfère à la figure 3, on doit donc avoir

\(\displaystyle \frac{L}{2} + l = \sqrt{2}\; (1)\).      (1)

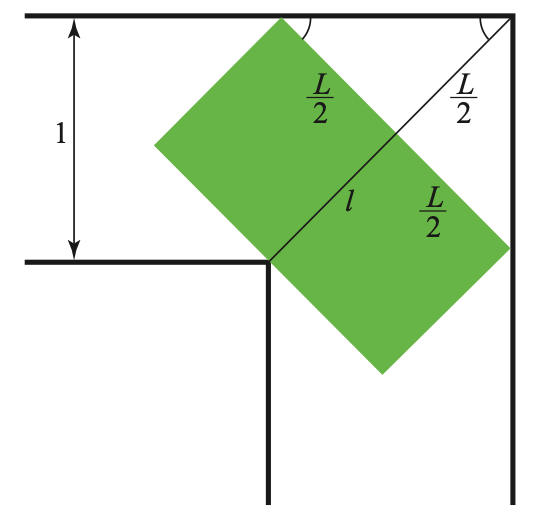
Figure 3. Visualisation de la formule (1)

Figure 3. Visualisation de la formule (1)

D’autre part, l’aire du sofa est \( A = L \times l \). Par (1), on a \( \times l \) = \( \sqrt{2} \) – \(\tfrac{L}{2}\) et donc

\( A = L\left(\sqrt{2} – \frac{L}{2}\right) = -\tfrac{1}{2}L^{2} + \sqrt{2}\,L \).      (2)

Pour quelles valeurs de L cette expression est-elle maximale ? C’est une expression de la forme \( f(x)=ax^{2}+bx+c,\ \text{où } a \) est négatif. On reconnaît le graphe d’une parabole ouverte vers le bas.  Le maximum se situe au sommet de la parabole et on l’obtient en faisant la complétion de carrés :

\( f(x)=a\!\left(x^{2}+\frac{b}{a}x+\frac{c}{a}\right) = a\!\left\{\left(x+\frac{b}{2a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4a^{2}}\right\}. \)

Le sommet de la parabole se situe au point \(x=-\frac{b}{2a}\) à la hauteur \( f\!\left(-\frac{b}{2a}\right)=c-\frac{b^{2}}{4a} \). Dans notre cas de figure, la forme de la parabole \( A(L) \) donnée en (2) est donc celle reproduite à la figure 4.

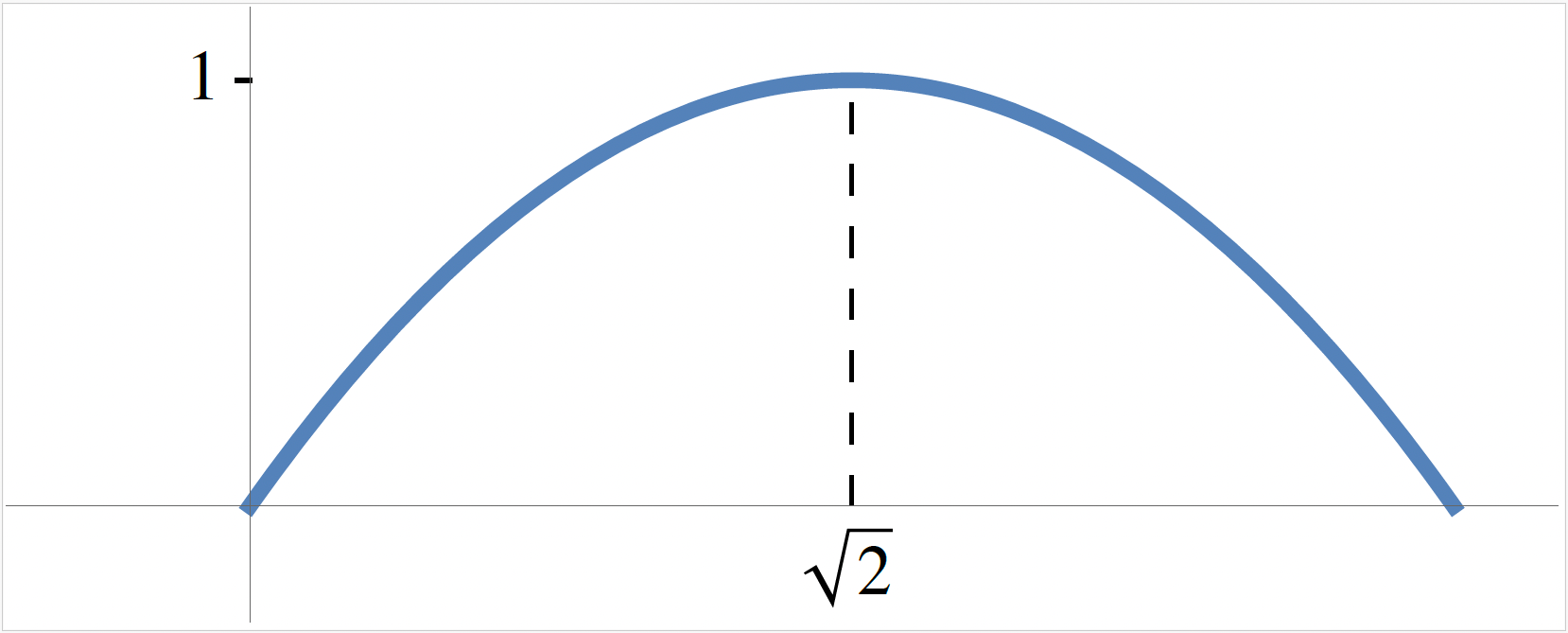
Figure 4. Tracé de \( A(L) \) en fonction de \( L \in [0,\,2\sqrt{2}] \).

Comme on peut le constater, la valeur maximale de l’aire se produit quand \(L=\) \(\sqrt[]{2},\) de sorte que

\(l=\sqrt[]{2}-\frac{\sqrt[]{2}}{2}= \frac{\sqrt[]{2}}{2}\)

La valeur maximale de l’aire vaut donc \(L ×l=\sqrt[]{2}×\frac{\sqrt[]{2}}{2}= 1\) Autrement dit, on n’a rien gagné… Le meilleur sofa rectangulaire n’a pas une aire supérieure au sofa carré, même s’il peut pivoter.

2e exploration : le sofa semi-circulaire

Une meilleure idée consiste à prendre un sofa en forme de demi-disque de rayon 1. Lorsqu’il atteint le coin, le demi-disque peut pivoter d’un quart de tour et ensuite glisser le long du corridor vertical (voir figure 5).

Figure 5. Déplacement d’un sofa semi-circulaire le long d’un corridor en L

Ce demi-disque a pour aire \(A=\frac{π}{2}≈1,5708.\) Cette fois, on a donc fait beaucoup mieux.

3e exploration : le sofa de Hammersley

En combinant l’idée d’un demi-cercle et celle d’un rectangle, le mathématicien britannique John Hammersley a proposé dès 1968 un sofa d’aire \(A=2,2074\). Pour ce faire, il a séparé le demi-disque de rayon 1 en deux quarts de disque et a inséré au milieu un rectangle de longueur \(L\) et de hauteur 1. Le résultat est un sofa dont le côté long mesure \(L\) + 2, tel qu’illustré à la figure 6.

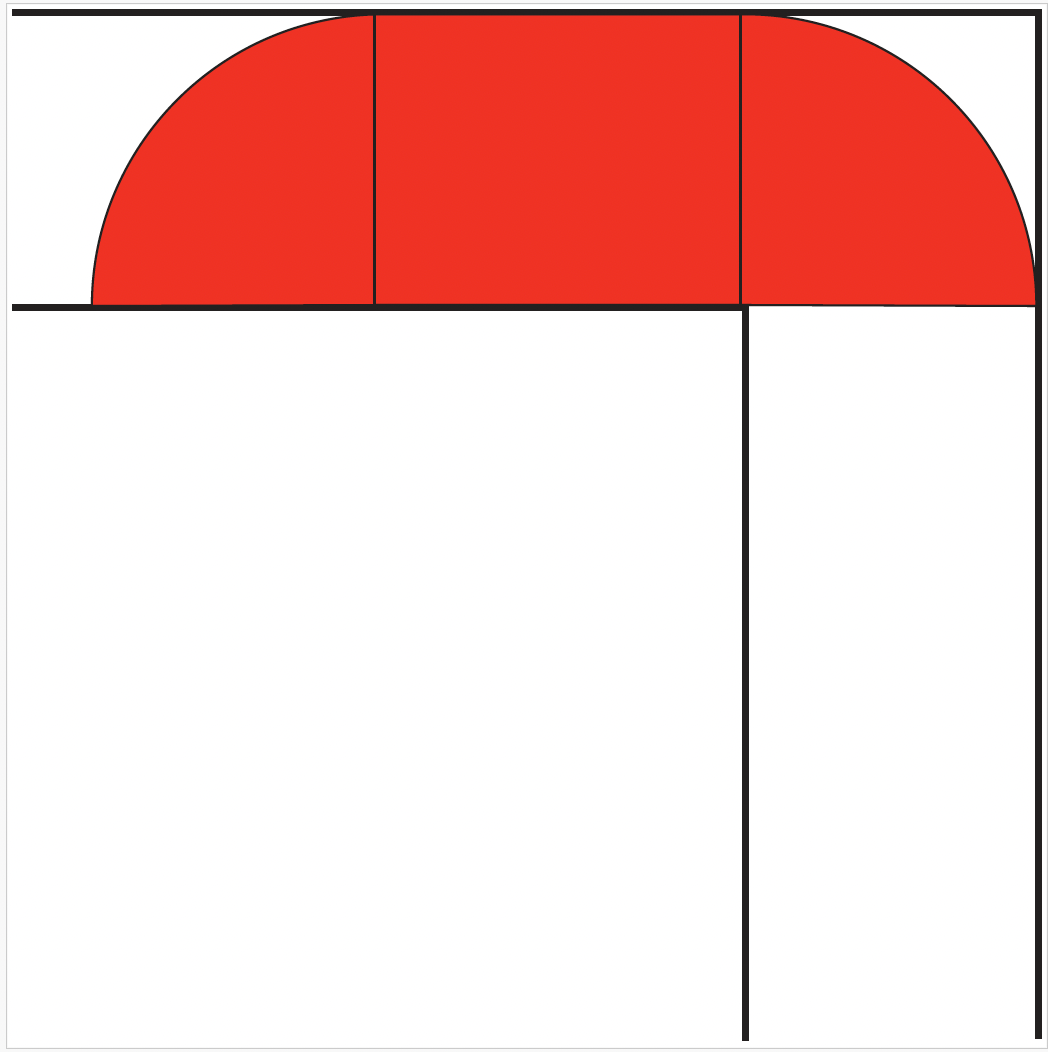
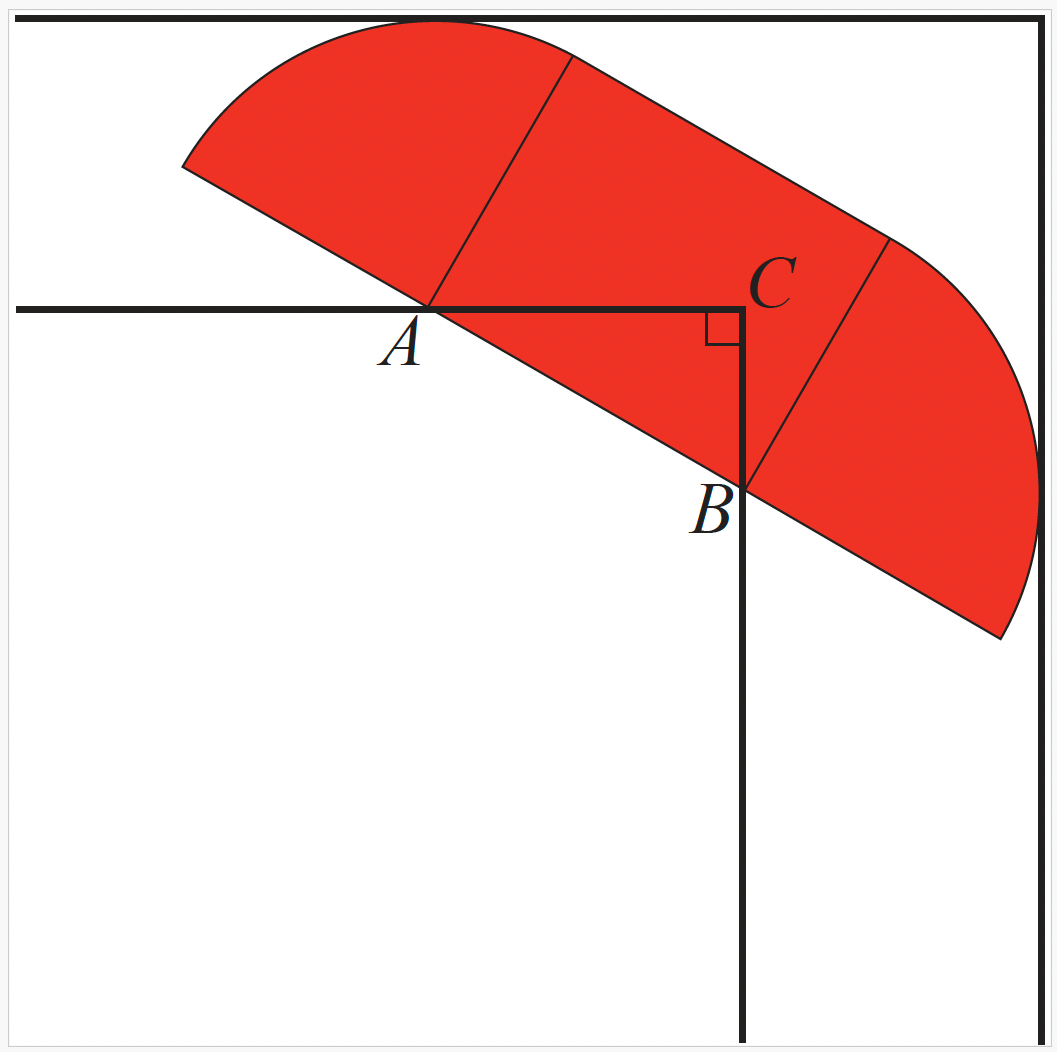
Figure 6. Tentative de déplacement d’un sofa composé d’un rectangle et de deux
quarts de disques le long d’un corridor en L

Cependant, en consultant la figure 6, on se rend vite compte que ce sofa ne peut pas passer le coin, sauf si on rogne à la base du rectangle tout ce qui l’empêche de pivoter. Pour toute rotation du sofa d’un angle entre \(0\)o et 90o, la partie qu’on doit rogner est le triangle rectangle \(ABC\) identifié dans la figure.

Remarquons que l’hypoténuse \(AB \) a toujours une longueur \(L  \). Les deux extrémités sont des quarts de cercle. Donc, leurs points sont à une distance 1 de \(A\) pour l’extrémité de gauche et à une distance 1 de \(B\) pour l’extrémité de droite. En particulier, lorsque le sofa se penche en roulant le long des quarts de cercle, tout en restant tangent aux deux murs extérieurs, les deux points \(A\) et \(B\) parcourent les murs intérieurs du corridor, dont la largeur est 1.

Si on place le segment \(AB\) à l’horizontale, quelle est la réunion de tous ces triangles \(ABC \) ? C’est simplement le demi-disque de diamètre \(AB\), comme on le voit à la figure 7. On utilise ici le fait qu’un angle inscrit dans un demi-cercle est un angle droit. En effet, il est égal à la moitié de l’angle au centre associé qui vaut \(180\)o.


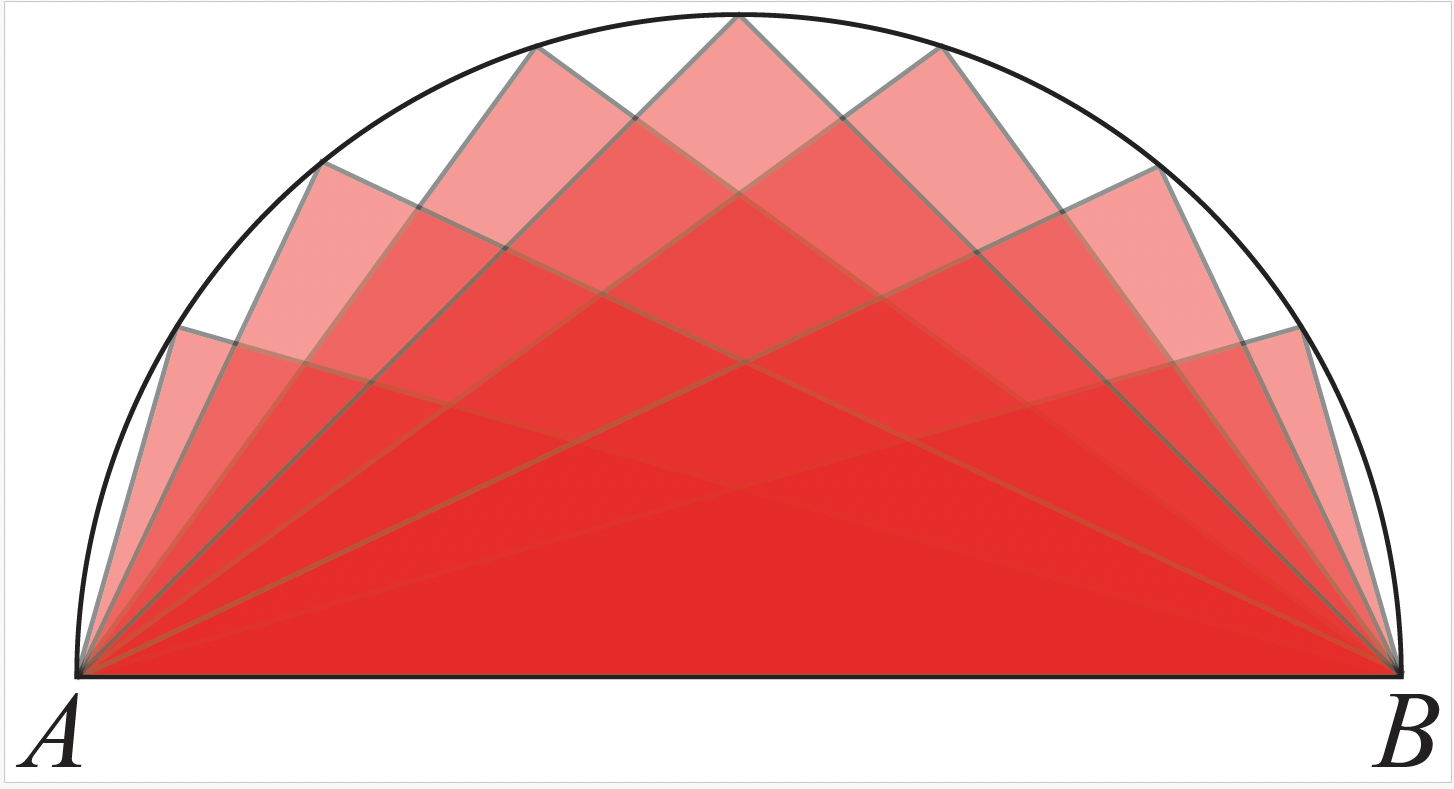
Figure 7. Parties du rectangle à rogner pour que le sofa puisse pivoter.

Finalement, on a un sofa d’une forme assez élégante, illustré à la figure 7. C’est le sofa de Hammersley.


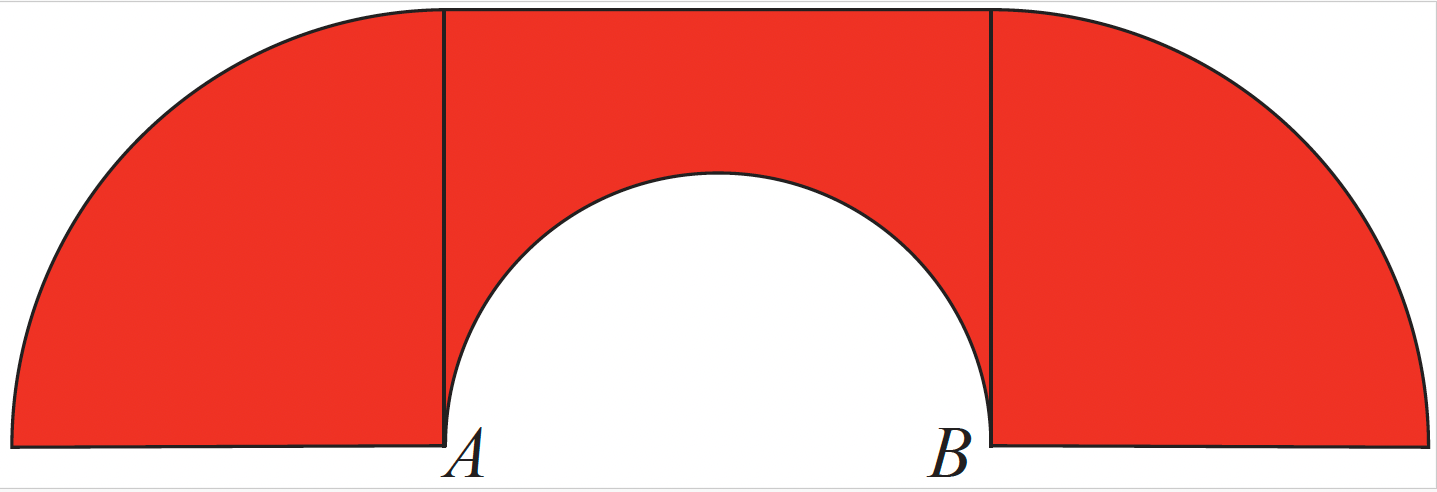
Figure 8. Le sofa de Hammersley.

Quelle est l’aire du sofa de Hammersley ? Ici encore, on peut proposer ce calcul sous forme de problème. La réponse se trouve ci-dessous.

Les deux extrémités sont des quarts de disque de rayon 1, et la somme de leurs aires est égale à \(\frac{π}{2}\). La partie centrale est un rectangle d’aire \(L\), auquel on a soustrait un demi-disque de rayon \(\frac{L}{2}\), et donc d’aire \( \frac{\pi L^{2}}{8} \). L’aire de la partie centrale est alors \(L-\frac{\pi L^{2}}{8} \)\(.\) L’aire totale du sofa de Hammersley est donc

\(A=-\frac{\pi L^{2}}{8}+L+\frac{π}{2}.\)            (3)

On voit qu’il faut que \(L ∈ [0,2[\) pour obtenir un sofa d’un seul tenant. On a donc construit toute une famille de sofas, soit un sofa pour chaque valeur de \(L.\)

Pour quelle valeur de \(L\) cette aire est-elle maximale ? L’expression (3) est à nouveau une expression quadratique de la forme \(f\left(x\right)=ax^{2}+bx+c\), où \(a\) est négatif. Or, on a vu précédemment que le maximum est atteint au point \(x=-\frac{b}{2a}\) et qu’il vaut\( f(-\frac{b}{2a})=c-\frac{b^{2}}{4a}\).

Dans notre cas particulier, le maximum est atteint en \( L=\frac{4}{π}\) et \(A=\frac{π}{2}+\frac{2}{π}≈2,20742.\)

On a vraiment un sofa d’aire bien plus grande que les précédents !


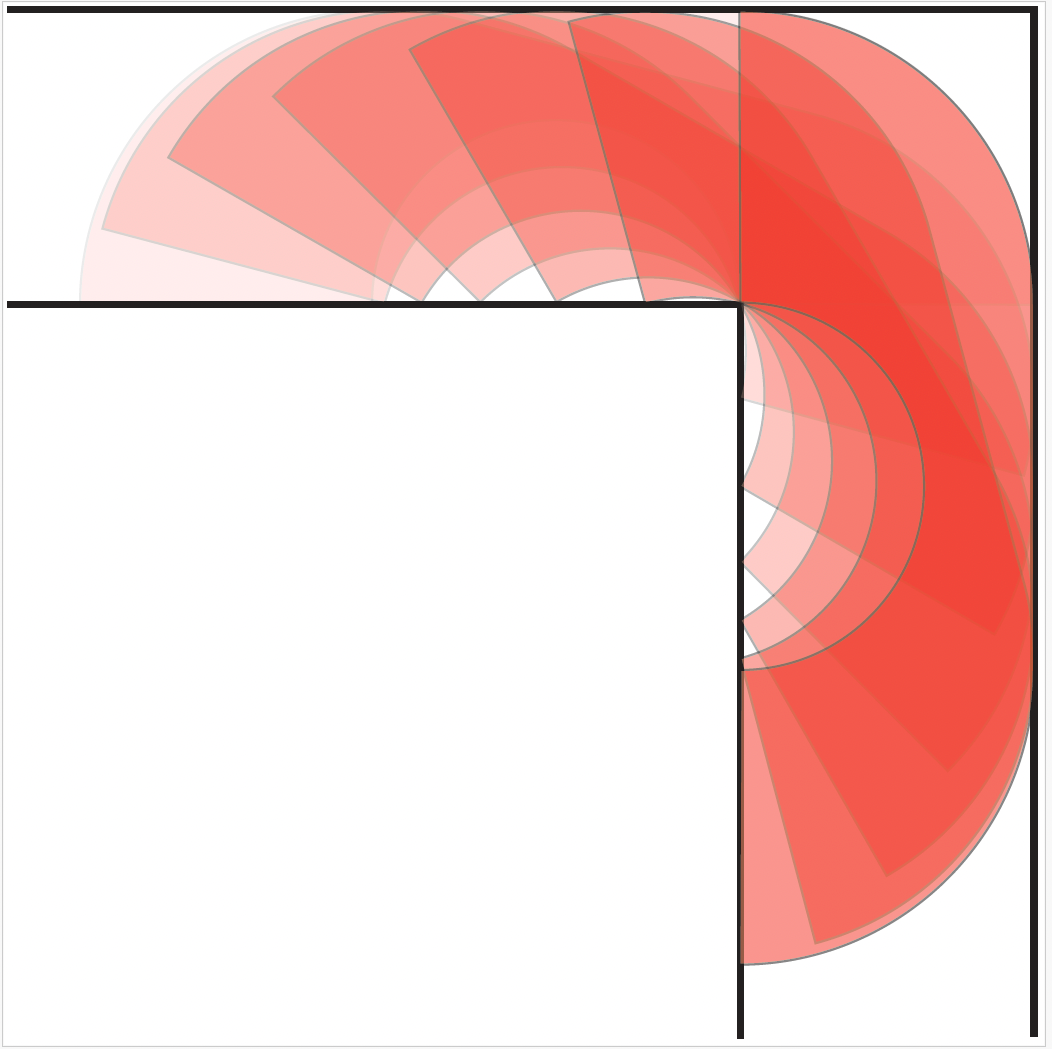
Figure 9. Déplacement d’un sofa de Hammersley le long d’un corridor en L

La figure 9 illustre plusieurs phases du pivotement du sofa de Hammersley dans le corridor. Le sofa touche aux quatre murs du corridor en tout moment2. Il n’y a donc aucune marge de manœuvre pour l’agrandir. Serait-il pour autant d’aire maximale ?

Une idée anodine qui se révèle très puissante

Jetons un second coup d’œil à la figure 7. Comment l’a-t-on réalisée ? On a considéré le sofa comme fixe et on a regardé toutes les positions du corridor tourné d’un angle quelconque entre 00 et 900 et contenant le sofa, comme à la figure 10. Si l’on y pense bien, un sofa d’aire maximale est exactement l’intersection de tous ces corridors tournés qui le contiennent. Car sinon, on pourrait augmenter le sofa de toute région contenue simultanément dans tous les corridors.


Figure 10. Les différentes positions du corridor autour du sofa fixe

 Raisonner en considérant un sofa fixe et un corridor qui tourne autour de lui est beaucoup plus facile que de faire tourner le sofa dans le corridor fixe. C’est le point de vue qui a été adopté pendant les décennies de recherche sur le sujet. En voici une première application.

Un sofa qui passe le coin a une aire maximale inférieure à \(2\sqrt[]{2}\) 

Est-on certain qu’un sofa d’aire maximale existe ou si on peut trouver des sofas de forme compliquée et d’aire arbitrairement grande ?

En exploitant l’idée du corridor tournant autour d’un sofa fixe, il est facile de montrer que, pour passer le coin, ce dernier doit nécessairement avoir une aire strictement inférieure à \(2\sqrt[]{2}≈2,828.\)

En effet, au départ, le sofa est dans la branche horizontale du corridor. Il peut tourner le coin de \(45\)o. Cela signifie qu’il est contenu dans l’intersection du corridor de largeur 1 et dans une translation du corridor tourné de \(45\)o. Quelques formes possibles de cette intersection sont illustrées à la figure 11.

Remarquons que plus le sommet du corridor est haut, plus l’aire de l’intersection est grande jusqu’à atteindre un plateau quand le coin intérieur du corridor tourné de \(45\)o est au sommet du corridor horizontal, comme il est illustré à la figure 12.

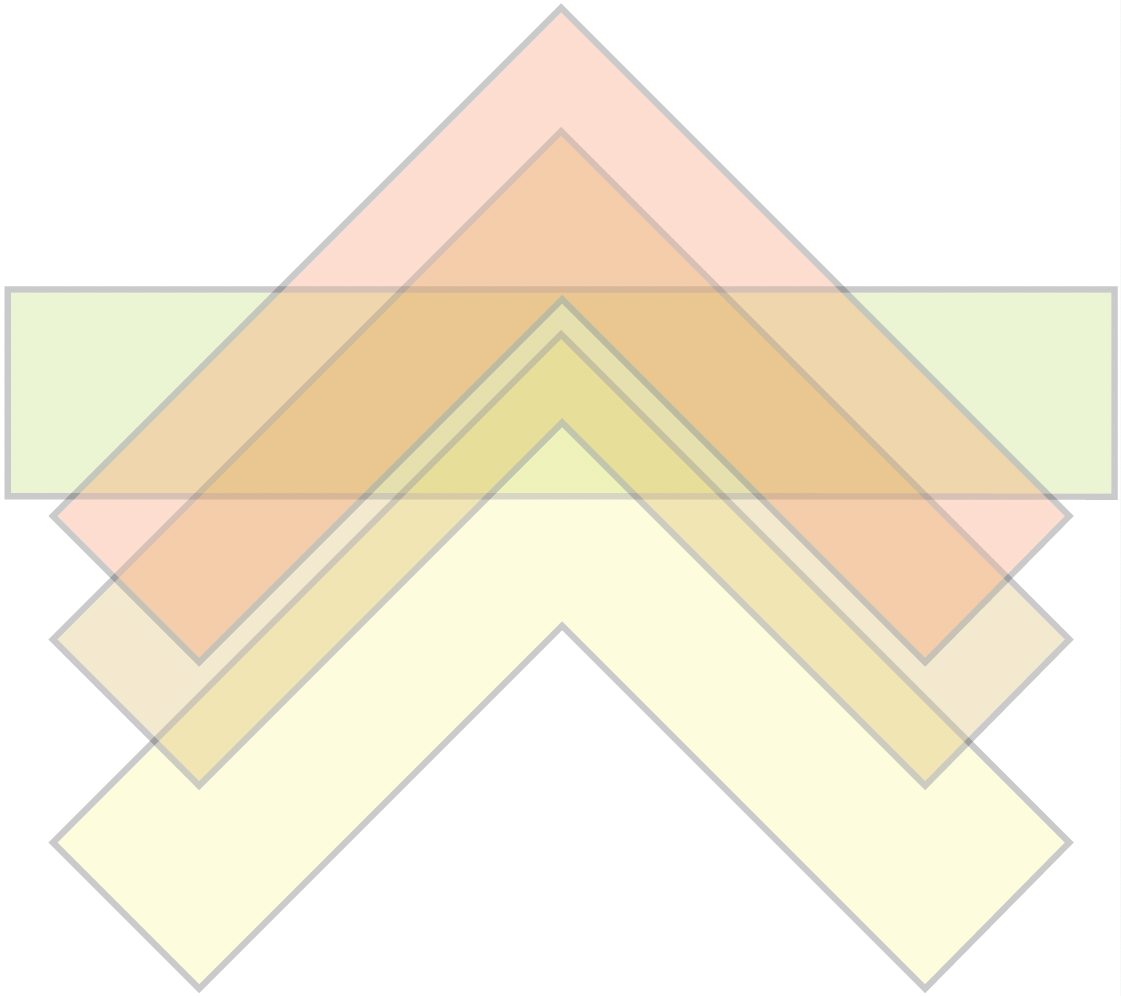Figure 11. Quelques intersections du corridor horizontal avec le corridor tourné de 45o


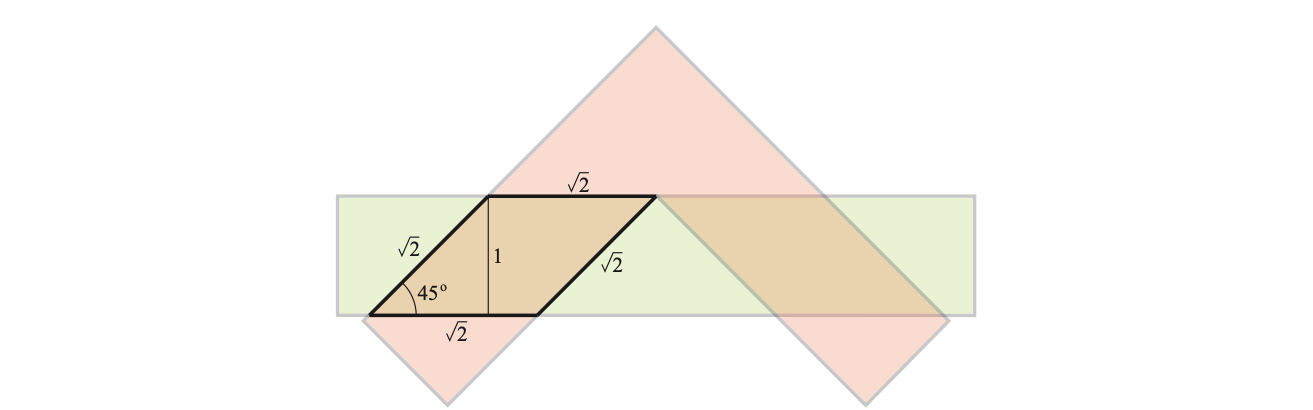
Figure 12. Une intersection d’aire maximale du corridor horizontal
avec le corridor tourné de 45o : elle est la réunion de deux losanges comme celui de gauche

Une telle position est impossible parce que le sofa serait alors scindé en deux parties. Toutefois, on peut s’en approcher aussi près que l’on veut avec un sofa très mince en son milieu. L’aire maximale d’un sofa passant le coin doit alors être inférieure à l’aire de cette intersection.

Cette intersection est la réunion de deux losanges3 de hauteur 1 et d’angle aigu de \(45\)o. La base a donc une longueur de \(\sqrt[]{2}\) et l’aire de chaque losange est \(\sqrt[]{2}\), puisque l’aire d’un parallélogramme est égale à sa base multipliée par sa hauteur (voir figure 13) et qu’un losange est un parallélogramme particulier.


Figure 13. L’aire d’un parallélogramme est égale à la base multipliée par la hauteur

Donc, l’aire de l’intersection des deux corridors est 2\(\sqrt[]{2}≈2,828.\) Ce raisonnement simple permet ainsi de conclure que l’aire maximale d’un sofa qui passe le coin est inférieure à 2,828.

L’aire du sofa comme Hammersley n’est pas maximale

Il a fallu attendre jusqu’en 1992 pour qu’un mathématicien américain, Joseph Gerver, donne une réponse négative à cette question en proposant un sofa d’aire 2,2195…, soit de l’ordre de 0,55 % fois plus grand que celui de Hammersley [6].

Le sofa de Gerver ressemble beaucoup au sofa de Hammersley, mais sa frontière, plus compliquée, est composée de 18 segments, tel qu’indiqué à la figure 14. Pour le bâtir, Gerver est parti du fait que le sofa de Hammersley touche aux murs inférieurs par des coins. Il s’est dit que si l’on rognait un peu ces coins, on pourrait épaissir le sofa du côté opposé et, ce faisant, en augmenter l’aire.

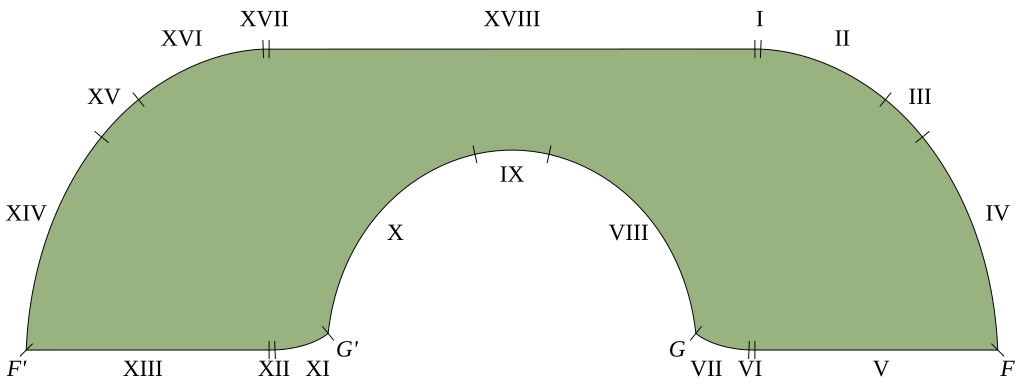
Crédit : TilmannR, Public domain, via Wikimedia Commons

Figure 14. Le sofa de Gerver

La concrétisation de cette idée est illustrée à la figure 15, dans laquelle les deux sofas sont superposés. Les aires en bleu sont celles que Gerver a rognées sur le sofa de Hammersley. Quant aux aires couleur saumon, elles montrent les gains que ces rognures ont permis de faire.

Figure 15. Superposition des sofas de Hammersley et de Gerver.
Les aires en bleu appartiennent exclusivement au premier,
tandis que celles qui sont couleur saumon appartiennent exclusivement au second.

Comment Gerver a-t-il construit son sofa ? C’est compliqué !

Pour une présentation en classe, il suffira sans doute de dire qu’à l’instar du sofa de Hammersley, le sofa de Gerver touche aux deux murs extérieurs du corridor dans chacune des positions lors du mouvement et que, dans presque toutes les positions, il touche aux murs intérieurs ou au coin intérieur4. Les 18 morceaux et 4 coins du sofa délimitant la frontière correspondent aux différentes manières dont le sofa touche les murs du corridor selon son angle. Les quarts de cercle et le demi-cercle inférieur du sofa de Hammersley sont remplacés par des courbes plus compliquées pour lesquelles il n’existe pas de formule explicite. Leur traçage requiert l’emploi d’un ordinateur, avec des instructions différentes dans chacun des 18 cas.

Pour plus de détails sur les grandes idées de la construction du sofa de Gerver, vous pouvez consulter l’article [5] publié en parallèle dans la revue Accromath, avec laquelle Envol collabore ici pour la première fois. Le sujet des mathématiques du sofa étant suffisamment riche pour intéresser des lectrices et lecteurs des niveaux secondaire, collégial et universitaire, les deux revues ont accepté de consacrer chacune un article à ce sujet, en le traitant à des niveaux de difficulté différents.

L’aire du sofa de Gerver est maximale ?

Ce n’est qu’en décembre 2024 que le jeune mathématicien coréen Jineon Baek a démontré dans un article de plus d’une centaine de pages que le sofa de Gerver avait effectivement une aire maximale [8]. En date du printemps 2025, l’article est en cours d’évaluation par les pairs, mais ses conclusions sont considérées comme crédibles par la communauté scientifique. Des arguments circonstanciels fondés sur l’apprentissage profond et renforçant cette conclusion ont en outre été mis en lumière par cinq chercheurs du Laboratoire Rutherford Appleton, à Didcot, au Royaume-Uni [7].

Conclusion

Le problème du sofa est un bel exemple de projet à présenter aux élèves. Il ouvre la voie à la résolution de problèmes intégrant plusieurs notions de mathématiques de niveau secondaire : géométrie euclidienne, sommet d’une parabole, complétion de carrés, etc. Il montre surtout que tout n’a pas été trouvé en mathématiques, y compris les réponses à des questions simples à énoncer et sur lesquelles les élèves pourraient proposer des approches originales et créatives.

[1] Une preuve rigoureuse nécessite le recours au calcul différentiel. On se contente donc d’expérimenter.
[3] Un losange est un parallélogramme dont tous les côtés sont de même longueur. 

[4] On peut visionner des animations de sofas de différentes formes parcourant le corridor à:

https://www.quantamagazine.org/the-largest-sofa-you-can-move-around-a-corner-20250214/. Une animation du sofa de Hammersley se trouve dans la référence[2]. Une animation du sofa de Gerver se trouve dans la référence [1] et https://www.youtube.com/watch?v=n5bMD3_JlFY&t=1s

Références

[1]  Sean Bailly, Le problème du sofa et celui du déménageur de piano enfin résolus, Pour la Science No 568, 8 février 2025.

[2]  Problème du sofa, Wikipedia, [https://fr.wikipedia.org/wiki/Problème_du_sofa].

[3]  Comment déménager un canapé dans les virages serrés ? Les mathématiques ont résolu ce problème, Science & vie, 17 décembre 2024,

[4]  Le problème mathématique du canapé est peut-être résolu pour de bon,

[5]  Le problème du sofa, C. Genest & C. Rousseau, Accromath, vol. 21, no 1 (printemps/été 2006), sous presse.

Références scientifiques (en anglais) sur le sujet

[6]  On Moving a Sofa Around a Corner, J.L. Gerver, Geom Dedicata (1992), vol. 42, no 3, pp. 267-283.

[7]  Deep Learning Evidence for Global Optimality of Gerver’s Sofa, K. Leng, J. Bi, J. Cha, S. Pinilla & J. Thiyagalingam, Symmetry (2024), vol. 16, no 10, 1388.

[8]  Optimality of Gerver’s Sofa, J. Baek, arXiv:2411.19826, prépublication.

Partagez

Articles dans ce numéro

Se connecter