Récit #5 d’une recherche-formation à l’enseignement
des probabilités avec des outils technologiques
Récit #5 d’une recherche-formation à l’enseignement des probabilités
avec des outils technologiques
Marche aléatoire
- 23 minutes de lecture

Mathieu Thibault
Mise en contexte
Je souhaite mettre de l’avant les réflexions menées par huit personnes qui ont participé à une recherche-formation à l’enseignement des probabilités avec des outils technologiques : cinq enseignant·es, deux conseiller·ères pédagogiques et un chercheur-formateur (moi-même). Une recherche-formation vise à répondre à la fois à des intentions de recherche, pour contribuer à l’avancement des connaissances, puis à des intentions de formation pour les personnes qui y participent en quête de développement professionnel. Celle-ci a été menée dans le cadre d’une recherche doctorale (Thibault, 2021). Les cinq séances de formation se sont déroulées à intervalles réguliers sur une période d’environ sept mois. Cinq récits de formation de cinq à huit pages ont ainsi été rédigés (disponibles à l’annexe F de Thibault, 2021) par le chercheur-formateur après chacune des séances, puis envoyés aux participant·es en vue d’être discutés à la séance suivante. On y retrouve plusieurs exemples des réflexions et discussions qui ont émergé des séances. Plus précisément, ces récits de formation sont constitués d’un itinéraire des situations probabilistes abordées, des ressources qui les accompagnent (matériel, simulateurs, etc.) ainsi que des idées importantes qui ont émergé en séance.
Dans cet article, le dernier d’une série de cinq, je présente les réflexions associées à un récit de formation qui a porté cette fois sur la situation de la marche aléatoire, dans l’environnement de programmation Scratch. On y retrouve de grandes idées évoquées lors de la séance de formation, notamment l’analyse didactique de la situation et des réflexions issues de l’expérimentation avec les participant·es, incluant un retour sur le potentiel de la programmation pour l’enseignement-apprentissage des mathématiques.
Situation de la marche aléatoire
Dans la recherche-formation, après avoir expérimenté les situations de Monty Hall (Thibault, 2023a), du jeu de dés (Thibault, 2023b), de la bouteille probabiliste (Thibault, 2024a) et des rondelles (Thibault, 2024b), les participant·es ont expérimenté la situation de la marche aléatoire. Préalablement à l’expérimentation de cette situation, les participant·es ont travaillé sur une tâche d’initiation à la programmation par blocs, par des commandes simples de déplacements, des boucles, puis des nombres aléatoires. L’objectif était de leur donner un aperçu pour les préparer à programmer un simulateur d’une expérience aléatoire à l’aide de l’environnement de programmation Scratch.
Puis, les participant·es ont expérimenté la situation de la marche aléatoire, dont l’énoncé est présenté dans l’encadré ci-dessous:

MARCHE ALÉATOIRE
Éric est debout sur une dalle appartenant à un petit trottoir. Il laisse le hasard guider ses pas en lançant une pièce de monnaie. Chaque fois qu’il obtient « pile », il avance d’une dalle. Quand il obtient « face », il recule d’une dalle.
Quelle est la probabilité qu’après quatre lancers, Éric soit revenu à son point de départ ?
*Programmez un simulateur pour reproduire cette situation et répondre à la question.
Cette situation est inspirée d’autres travaux qui ont eu recours à des marches aléatoires sous diverses versions (Gadanidis et al., 2016 ; Hernandez et al., 2010 ; Huerta, 2018 ; Pfannkuch et al., 2016). Pour réaliser cette situation, les participant·es, qui sont des enseignant·es et conseiller·ères pédagogiques d’expérience, ont travaillé en équipe de deux (comme on pourrait le faire dans une classe). Contrairement aux situations précédentes, aucun matériel ne leur a été fourni pour cette situation, alors que seul Scratch a été utilisé.
Analyse didactique de la situation
Pour réaliser cette tâche, il est attendu de programmer un simulateur qui reproduit une marche aléatoire, puis d’observer à l’aide d’une fréquence stabilisée qui permettrait d’estimer la probabilité de revenir au point de départ après quatre déplacements. S’il est programmé adéquatement, les résultats obtenus par ce simulateur dans l’approche fréquentielle devraient fournir une tendance suggérant que la probabilité semble être d’environ 35 %-40 %.
Par l’approche théorique, un diagramme en arbre de 4 lancers de pièce de monnaie fait ressortir 16 cas possibles (source : DUDAMATH – action zone).
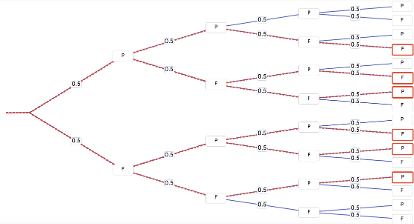
En fait, pour revenir au point de départ, il faut obtenir autant de résultats « pile » que de résultats « face », c’est-à-dire autant de déplacements vers l’avant que vers l’arrière, ce qui se produit dans 6 des 16 cas (identifiés en rouge dans le diagramme en arbre). La probabilité de revenir au point de départ après quatre déplacements est donc de \(\frac{6}{16}\) (ou 38 ou 37,5 %). Il est aussi possible d’avoir recours à l’approche subjective, en émettant une prédiction (qualitative ou quantitative), qui pourrait même se raffiner au fur et à mesure que de nouvelles informations sont obtenues.
Analyse didactique de la programmation avec Scratch
Scratch, disponible en ligne, offre un langage de programmation visuel qui facilite l’initiation à la programmation. En effet, cet environnement de programmation amène une « approche d’apprentissage procédurale de la programmation par assemblage de blocs de programmation pas à pas que l’on peut comparer à la construction d’un casse-tête » (Romero, 2016, p. 88). De cette façon, ce n’est pas le langage de programmation qui doit être appris, alors que cela représentait par le passé une des difficultés. En effet, des tentatives d’enseignement à l’aide de la programmation ont été tentées en vain depuis les années quatre-vingt, car la courbe d’apprentissage était trop exigeante alors qu’il fallait d’abord se former à la programmation (et ne surtout pas oublier un « ; » sans quoi le programme ne s’exécutait pas !) avant de pouvoir faire des mathématiques.
La programmation par blocs amène un regain d’intérêt et une simplification des usages pour programmer, mais il reste à voir si les avantages vont surpasser les défis. Les défis à envisager concernent notamment l’exploration et l’intégration de la programmation pour l’enseignement des probabilités. En effet, comme pour toute nouvelle ressource, les personnes participantes peuvent avoir besoin de temps et d’accompagnement pour se les approprier. De plus, elles peuvent avoir besoin d’être convaincues de la valeur ajoutée de la programmation par rapport au papier-crayon, alors que cela peut être perçu comme un ajout en plus de devoir travailler toutes les notions mathématiques qui sont prescrites par le Programme de formation de l’école québécoise en mathématiques au secondaire (gouvernement du Québec, 2006, 2016).
Expérimentation avec les participant·es
Lorsque la situation des marches a été expérimentée avec les participant·es de la recherche-formation, le chercheur-formateur (moi-même) a donné accès à la mise en situation ainsi qu’à Scratch.
Florence et Déborah (pseudonymes) ont travaillé en équipe, mais elles ont rapidement constaté qu’elles avaient des manières différentes de travailler. Florence avait besoin de résoudre cette tâche à l’aide de l’approche théorique. Elle a alors fait un diagramme en arbre et a constaté qu’il faut obtenir deux fois pile et deux fois face (sans tenir compte de l’ordre) pour revenir au point de départ après quatre lancers de pièce de monnaie. Florence a alors dénombré 6 cas favorables sur 16 cas possibles, pour une probabilité de \(\frac{6}{16}\). De son côté, Déborah préférait se faire un plan de programmation pour pouvoir se lancer dans Scratch. Il n’est toutefois pas facile de faire ce plan, car des bases en programmation sont requises pour savoir ce dont on a besoin pour faire ce plan. Pour Déborah, il était nécessaire de voir d’abord les options de blocs avant de commencer le programme. Elle a alors consulté un document avec tous les blocs possibles dans Scratch pour repérer les blocs dont elle pourrait avoir besoin. Florence disait plutôt ne pas avoir besoin de plan et préférait y aller à tâtons dans Scratch, après avoir déterminé la probabilité théorique. Ensuite, pour simuler le déplacement en générant le résultat d’une pièce de monnaie, Florence a hésité sur la façon de générer un résultat de pièce de monnaie, puis en est venue à la conclusion qu’il fallait choisir un nombre entier aléatoire entre 1 et 2. Pour chacun des deux nombres possibles, elle a attribué l’action d’avancer (pile) ou de reculer (face).
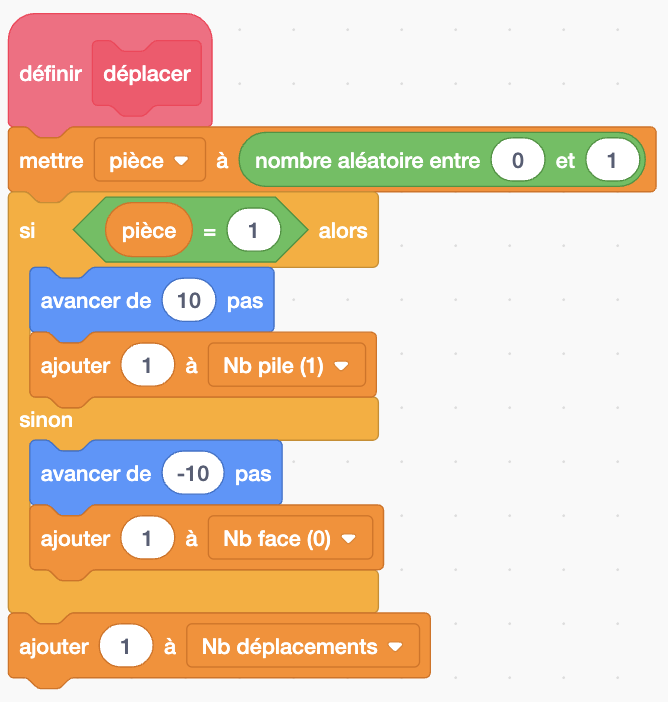
Après avoir conçu un programme qui permet au personnage de se déplacer quatre fois à l’aide d’une boucle, puis de vérifier s’il revient au point de départ (si le nombre de pile est égal au nombre de face), Déborah voulait faire calculer la fréquence basée sur les résultats expérimentés. Lorsqu’elles y sont parvenues, Déborah et Florence étaient d’avis qu’elles se sont bien complétées, en ne travaillant pas de la même façon : Déborah préférait commencer son programme globalement pour ensuite préciser les détails qui se trouvent à l’intérieur, alors que Florence préférait commencer sur des parties en détail, puis d’élargir en ajoutant des couches au programme.
Grace et Émilie ont formé une autre équipe et ont commencé par établir un plan de programmation pour identifier les variables nécessaires et la structure générale du programme. Pour générer le résultat d’une pièce de monnaie, Grace et Émilie ont été un peu bloquées. Le chercheur a alors précisé que la seule façon d’avoir du hasard dans Scratch est d’utiliser le bloc de nombre aléatoire. Grace a alors pu générer un nombre aléatoire entre 1 (pile) et 2 (face). Elles ont créé une variable pour compter le nombre de pile, puis une autre variable qui dénombre le nombre de face, mais cette fois dans les nombres négatifs. Ainsi, elles ont additionné les résultats de ces variables et Émilie a expliqué que le programme vérifie si cette somme est égale à zéro pour savoir si le personnage revient au point de départ. C’est donc l’idée d’avancer (+1 pour pile) et de reculer (-1 pour face). Grace a précisé que cela revient à voir le déplacement du personnage sur une droite numérique. En s’appuyant seulement sur les valeurs des variables (sans faire déplacer le personnage), Émilie a testé le fonctionnement de leur programme : elle a obtenu 3 résultats favorables sur 10 essais, alors la fréquence observée était de \(\frac{3}{10}\). Elles ont ensuite testé 10 échantillons de 100 essais en notant les fréquences, avec l’aide du chercheur-formateur pour garder une trace des résultats des simulations dans une liste. Grace a remarqué que les fréquences étaient d’environ 0,4. Émilie a complété un diagramme en arbre et a obtenu elle aussi une probabilité de \(\frac{6}{16}\)=0,375, ce qui leur a permis de comparer la probabilité théorique aux fréquences observées. En simulant le programme plusieurs fois, les résultats s’ajoutaient chaque fois dans la liste et Émilie a fait remarquer que ces fréquences sont assez près de la probabilité théorique. Grace et Émilie ont ensuite calculé la moyenne de leurs essais répertoriés dans la liste, soit la moyenne des fréquences obtenues, qui devrait normalement être une estimation encore plus fiable de la probabilité, en raison de la loi des grands nombres.
Si on compare ce qui a été fait par ces deux équipes, on constate des différences entre les programmes. Par exemple, pour vérifier si le personnage revient au point de départ, Florence et Déborah ont vérifié si les variables du nombre de pile et du nombre de face sont égales, ce qui est différent (mais équivalent) à vérifier si la somme est nulle avec des nombres positifs et négatifs, comme l’ont fait Grace et Émilie. On pouvait même utiliser une seule variable, comme Brian l’a fait, en ajoutant 1 lorsqu’on obtient 1 (pile) et en enlevant 1 lorsqu’on obtient 2 (face), puis en vérifiant si la valeur finale est égale à zéro après quatre déplacements. Une autre différence concerne l’aspect visuel : pour le programme de Florence et Déborah, ainsi que celui de Christian, le personnage effectuait les déplacements tels qu’expliqués dans la mise en situation. Quant au programme de Grace et Émilie, il effectuait simplement les calculs à partir des variables, sans représenter les déplacements, ce qui permettait d’effectuer des simulations plus rapidement, en se détachant de chaque lancer individuel de pièce de monnaie.
Il existe donc une multitude de façons différentes d’écrire un programme (et donc une multitude de solutions au problème), selon le choix des variables, les vérifications des conditions et le niveau de flexibilité qui est accordée à l’utilisateur du programme qui est produit. Il faut donc penser à plusieurs aspects en même temps pour que le programme fonctionne et il est possible d’avoir une approche plus globale ou par parties, ce qui amène des allers-retours pour lesquels il faut constamment s’ajuster. Il faut aussi être inventif pour trouver une façon de générer l’équivalent d’un choix (pile ou face) à l’aide d’un bloc de nombres aléatoires. En concevant un simulateur, il semble y avoir une réelle appropriation des possibilités du simulateur et des prolongements pourraient être expérimentés aussitôt.
Il a d’ailleurs été question des prolongements possibles pour cette situation, de manière à la complexifier. En voici quelques suggestions:
- Le nombre de lancers pourrait être modifié (six lancers au lieu de quatre ou encore généraliser à n lancers) ;
- Une troisième option (par rapport à avancer ou reculer) pourrait être de rester sur place ;
- On pourrait considérer quatre options (haut, bas, gauche ou droite), ce qui amènerait à se déplacer sur le plan dans les quatre directions ;
- On pourrait plutôt s’intéresser au nombre de déplacements nécessaires pour revenir au point de départ.
Selon le prolongement, il s’agit parfois d’un simple ajustement dans le programme. Par exemple, pour le nombre de déplacements, il est facile de modifier la boucle afin qu’elle se répète six fois au lieu de quatre. Pour d’autres prolongements, cela demanderait davantage d’ajustements.
Pour le troisième prolongement, voici un exemple de programme qui simule une marche aléatoire dans les quatre directions. On reconnaît la structure du programme, mais le problème devient tout de même assez différent.
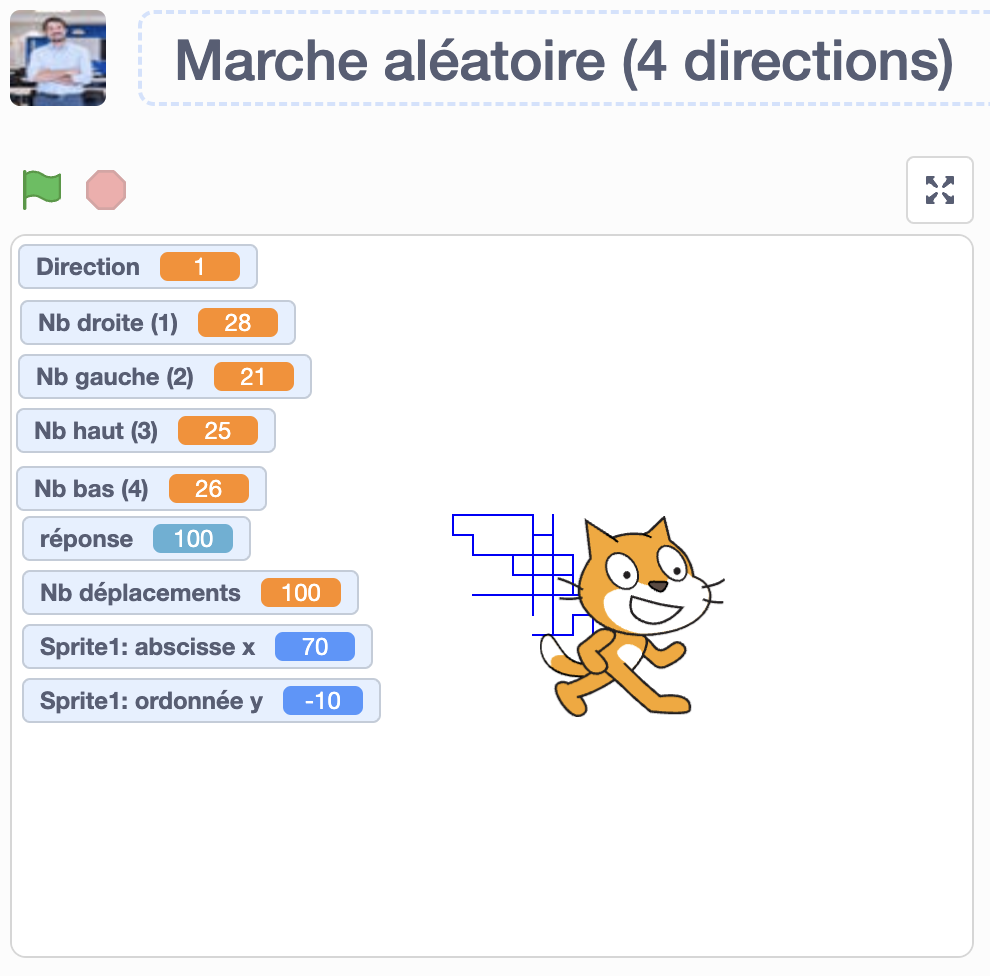
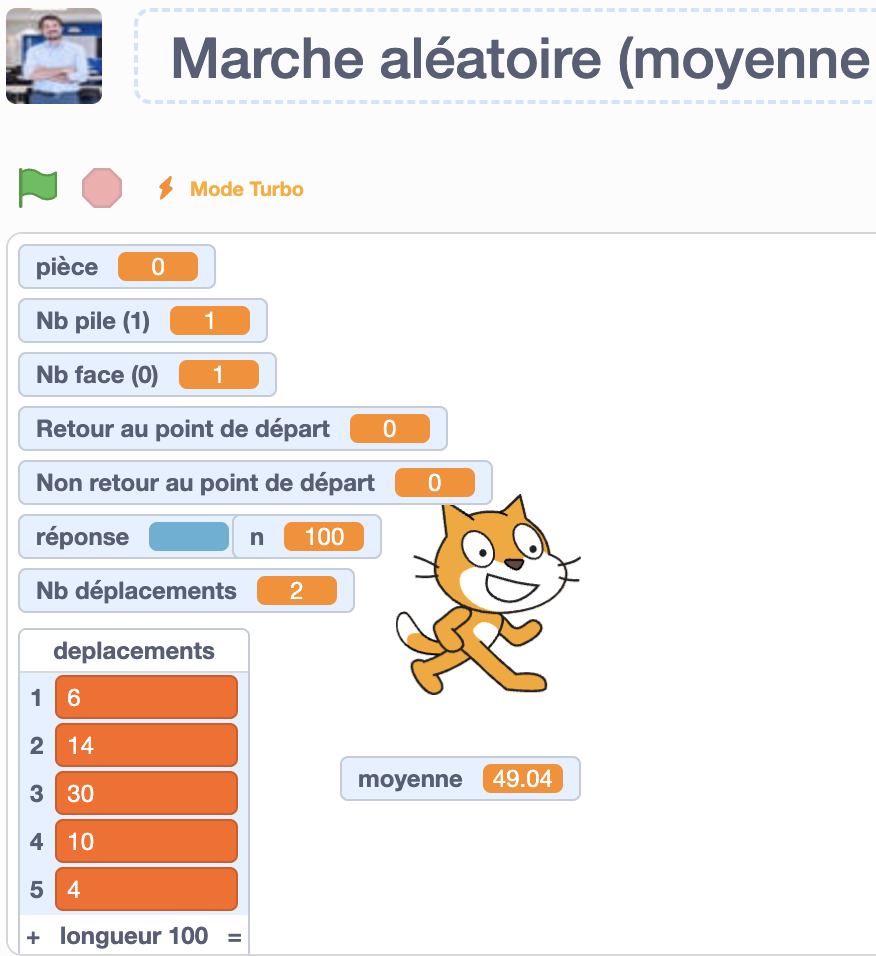
En ce qui concerne le quatrième prolongement, ce simulateur calcule la moyenne de la longueur des déplacements nécessaires afin de revenir au point de départ, dans une marche aléatoire simple (avancer et reculer). Il est à noter que le personnage peut parfois se déplacer pendant très longtemps, alors il est préférable d’aller « voir à l’intérieur » et d’enclencher le mode turbo pour que cela s’exécute en moins d’une seconde. Pour résoudre ce problème théoriquement, il faudrait effectuer des calculs de sommes infinies, ce qui serait très complexe, alors on peut plutôt regarder ce qui se passe en pratique avec un tel simulateur. On constate avec surprise que les résultats obtenus des longueurs de déplacements ne semblent pas converger : 7044, 7345, 64, 200, 23 604, 40… Il est à noter que la simulation est parfois longue lorsque le personnage se rend très loin du point de départ, car cela lui prend beaucoup de déplacements pour revenir.
Réflexion sur les enjeux de la programmation pour l’enseignement des probabilités
Dans la séance, le chercheur-formateur a questionné les participant·es quant aux enjeux de la programmation pour enseigner les probabilités. Selon Florence, la programmation était difficile pour elle, alors elle concevait mal comme l’élève pourrait y apprendre en mathématiques. Pour Déborah, c’est une façon pour l’élève d’apprendre à raisonner. Elle a même suggéré que la programmation nous permet d’aller plus loin dans notre réflexion et que l’on fait preuve de compréhension lorsqu’on arrive à programmer le simulateur. Toutefois, Christian a mentionné que certains bogues ne concernent pas la compréhension des probabilités, mais plutôt l’aspect technique de la programmation. De plus, il est possible d’utiliser des programmes déjà faits et de les utiliser tel quel ou encore de les bonifier, au lieu de repartir d’une page vide. C’est d’ailleurs l’idée de Scratch de ne pas nécessairement partir « from scratch » (de rien) en pouvant partager publiquement les programmes créés pour qu’ils soient utiles à d’autres personnes.
Florence a alors soulevé le questionnement quant à savoir « Pour qui est la programmation ? ». Est-ce pour l’apprenant·e en général, donc autant pour l’élève que l’enseignant·e ? En raison des difficultés déjà évoquées, il serait possible de penser que seulement l’enseignant·e peut être en mesure de programmer, en préparant des programmes qui peuvent être utilisés par les élèves. Toutefois, on peut penser que même l’élève pourrait bénéficier de l’apprentissage lié à la programmation, où le fait de concevoir un programme plutôt que de simplement l’utiliser amènerait à réfléchir à des caractéristiques d’une expérience aléatoire.
L’apprentissage par la programmation amène aussi des défis non négligeables autant pour l’élève que pour l’enseignant·e qui doit réunir des conditions favorables pour accompagner cet apprentissage. Le développement de la compétence à programmer nécessite du temps. La contrainte de temps a d’ailleurs été évoquée par plusieurs, mais certain·es étaient d’avis que le jeu en valait la chandelle, car cela est amusant pour les élèves. Cet aspect de plaisir est d’ailleurs ressorti durant la séance, car tous ont préféré continuer de travailler sur leur programme au lieu de prendre une pause !
À la séance suivante, soit la dernière de la recherche-formation, un retour a permis de revenir sur les enjeux de la programmation pour l’enseignement des probabilités. Grace a apprécié avoir pris le temps d’aborder Scratch dans un contexte de résolution de problème, où il y avait des contraintes et un but à atteindre, mais plusieurs façons de s’y rendre. Elle a ajouté que la programmation permet tout de suite de voir s’il y a une erreur si le programme ne fonctionne pas comme on le souhaiterait, alors cette rétroaction permet de se réajuster immédiatement. En ce sens, le statut de l’erreur est différent en programmation étant donné que c’est un peu comme un jeu : si on se trompe, ce n’est pas grave et on essaie encore. Comme le disait Christian, c’est juste un bogue ! Par contre, il a été soulevé que certains bogues peuvent parfois nous bloquer à faire des mathématiques (ou plus particulièrement des probabilités). Malgré ce défi, les personnes participantes étaient toutes intéressées à l’intégrer éventuellement dans leur pratique d’enseignement.
De plus, toutes les personnes participantes étaient d’avis que les élèves devront éventuellement apprendre à programmer à l’école et Brian a même affirmé que ceux qui ne sauront pas programmer au 21e siècle seront un peu démunis, car il s’agit d’une compétence indispensable à développer. Grace a ajouté que les métiers de demain vont tourner autour de la technologie, alors la programmation est un incontournable. Cependant, elle a fait remarquer que l’on a encore du mal à l’intégrer dans nos pratiques puisque l’on a du mal à sortir de notre zone de confort, en raison de certaines réticences liées à l’enseignement à l’aide de la programmation. Il s’agit d’ailleurs d’un constat qui découle de cette recherche : le recours à la programmation dans des séances de formation peut amener des enseignant·es à reconsidérer leur enseignement. En effet, des personnes participantes ont d’abord exprimé beaucoup de réserves et de questionnements, laissant croire qu’elles n’étaient pas prêtes à envisager l’intégration de la programmation dans leur enseignement. Cependant, lors de la séance suivante, elles se sont toutes positionnées en faveur de la programmation pour la classe de mathématiques dans un avenir plus ou moins lointain. Il était même étonnant de constater que l’enseignante qui semblait la plus sceptique envers la programmation a continué de poursuivre son exploration et a même donné par la suite un atelier de formation continue sur la programmation pour l’enseignement des mathématiques. Donc, en ce qui concerne la programmation pour l’enseignement des mathématiques, quand j’écrivais plus tôt qu’il reste à voir si les avantages vont surpasser les défis, il semble que ce soit le cas, du moins pour ces participant·es !
Il a aussi été question de programmation pour pouvoir modifier des outils existants afin qu’ils puissent mieux répondre à nos besoins spécifiques en enseignement des mathématiques. À ce sujet, Alan a dit qu’il est important de produire des outils utiles, polyvalents et de qualité, qui pourront alors être utilisés pendant longtemps par plusieurs personnes. Selon Brian, on gagnerait à ce que ces outils créés par des enseignant·es soient partagés et diffusés pour en faire bénéficier le plus grand nombre. Force est de constater que le partage a bien évolué dans les dernières années dans la communauté d’enseignant·es de mathématiques, ce qui est inspirant ! D’ailleurs, si vous avez des idées probabilistes à partager à la communauté, n’hésitez pas à le faire sur le groupe Facebook « Pour l’amour de l’enseignement des probabilités ! ». Plusieurs ressources qui ont été partagées dans ce groupe ont été répertoriées et organisées sur un site, dont des tâches, articles, capsules vidéos et outils technologiques qui sont accessibles à toute personne intéressée à l’enseignement-apprentissage des probabilités.

Conclusion
Selon les participant·es de cette recherche-formation, la programmation s’avère une activité pertinente pour faire des mathématiques en général et des probabilités en particulier. En effet, la programmation permet de créer de nouvelles ressources ou de modifier des ressources existantes pour soutenir la compréhension, pour permettre une validation et pour consolider ou même enrichir certains apprentissages. Il s’agit donc d’une compétence à développer chez les élèves et les enseignant·es, qui gagnerait à être reconnue dans le Programme de formation de l’école québécoise en mathématiques au secondaire (gouvernement du Québec, 2006, 2016). Il semble important que la programmation soit aussi faite par les élèves, qui apprennent davantage quand ce sont eux qui en font, mais pour cela il faut que les enseignant·es soient formé·es à accompagner leurs élèves.
Pour en apprendre un peu plus sur la programmation par blocs pour apprendre en probabilités, le chapitre de Venant et Thibault (2019) pourrait vous intéresser.
Références
- Gadanidis, G., Hughes, J. M., Minniti, L. et White, B. J. (2016). Computational thinking, grade 1 students and the binomial theorem. Digital Experiences in Mathematics Education, 3 (2), 77-96. https://doi.org/10.1007/s40751-016-0019-3
- Gouvernement du Québec. (2006). Programme de formation de l’école québécoise : enseignement secondaire, premier cycle. Québec : Ministère de l’Éducation. http://www.education.gouv.qc.ca/fileadmin/site_web/documents/PFEQ/prfrmsec1ercyclev2.pdf
- Gouvernement du Québec. (2016). Programme de formation de l’école québécoise : enseignement secondaire, deuxième cycle. Québec : Ministère de l’Éducation, du Loisir et du Sport. https://cdn-contenu.quebec.ca/cdn-contenu/education/pfeq/secondaire/PFEQ-presentation-deuxieme-cycle-secondaire.pdf
- Hernandez, T. H. M., Kataoka, V. Y. et de Oliveira, M. S. (2010). Random walks in teaching probability at the high school. Dans M. A. Sorto, A. White et L. Guyot (dir.), Looking back, looking forward. Proceedings of the Tenth International Conference on Teaching Statistics (ICOTS10). Kyoto : International Statistical Institute. https://iase-web.org/documents/papers/icots8/ICOTS8_2B1_HERNANDEZ.pdf?1402524969
- Huerta, P. M. (2018). Preparing teachers for teaching probability through problem solving. Dans C. Batanero et E. J. Chernoff (dir.), Teaching and Learning Stochastics (p. 293-311). Springer, Cham. https://link.springer.com/chapter/10.1007/978-3-319-72871-1_17
- Pfannkuch, M., Budgett, S., Fewster, R., Fitch, M., Pattenwise, S., Wild, C. et Ziedins, I. (2016). Probability modeling and thinking: What can we learn from practice? Statistics Education Research Journal, 15(2), 11-37. https://www.researchgate.net/publication/316961423
- Romero, M. (2016). De l’apprentissage procédural de la programmation à l’intégration interdisciplinaire de la programmation créative. Formation et profession, 24 (1), 87‐89. https://doi.org/10.18162/fp.2016.a92
- Thibault, M. (2021). Recherche-formation sur l’enseignement des probabilités du secondaire avec des outils technologiques : enjeux de formation. Thèse de doctorat. Université du Québec à Montréal. https://www.researchgate.net/publication/356145559
- Thibault, M. (2023a). Récit #1 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Monty Hall. Envol, 181, 30-35. https://www.researchgate.net/publication/370320198
- Thibault, M. (2023 b). Récit #2 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Jeu de dés. Envol, 182, 6–11. https://www.researchgate.net/publication/374951685
- Thibault, M. (2024a). Récit #3 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Bouteille probabiliste. Envol, 183, 12–19. https://www.researchgate.net/publication/380167138
- Thibault, M. (2024 b). Récit #4 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Rondelles. Envol, 184, en ligne : https://revueenvol.ca/envol-membres/numero-184/recit-4-dune-recherche-formation-a-lenseignement-des-probabilites-avec-des-outils-technologiques-rondelles/
- Venant, F. et Thibault, M. (2019). Programmer pour apprendre en probabilités. Dans V. Martin, M. Thibault et L. Theis (dir.), Enseigner les premiers concepts de probabilités : un monde de possibilités ! (p. 271-297). Québec : Presses de l’Université du Québec.
Articles dans ce numéro

Mot de la Directrice
Il me fait plaisir de vous présenter votre tout nouveau numéro de la revue Envol,

Le GRMS : Alimenter la réflexion
Je suis heureux de vous présenter ce nouveau numéro de notre revue, un moment privilégié

Hommage à Pierre Couillard, plus qu’un « brancheux » de fils
Son entrée dans le monde de l’éducation, à la fin des années 1980, où les

La classe collabo-réflexive en mathématiques : un bref survol
Une classe collabo-réflexive se distingue par son dynamisme : les élèves, debout et répartis dans

La partie entière, tranchée mince : une approche BTC en action
Ce chapitre explique comment maintenir l’intérêt des élèves grâce au « thin slicing », illustré

Desmos Mode Examen : un outil équitable pour soutenir l’évaluation en mathématique et favoriser la réussite
Parmi les outils numériques disponibles, la calculatrice graphique de Desmos s’est rapidement imposée comme une

Évaluer autrement: tâche flexible, créative et colorée en mathématiques CST et TS de cinquième secondaire
Probablement comme plusieurs d’entre vous, nous trouvons important de présenter à nos élèves des tâches

Parole aux communautés de pratique interordres secondaire-collégial en mathématiques
Comment faciliter la transition secondaire-collégial en mathématiques des élèves finissants de 5e secondaire qui feront

Leçons de la classe de mathématiques
L’après-midi bat son plein et les élèves travaillent fort à résoudre les tâches que je
Un codage à la Gödel
Le but de ce court texte est de partager une idée avec laquelle j’avais jonglé

La manipulation au secondaire : est-ce vraiment nécessaire ?
Lors du dernier congrès du GRMS, Geneviève Dupuis, conseillère pédagogique du Récit de l’enseignement privé,

5e article: la marche aléatoire (probabilltés)
Récit #5 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Marche aléatoire

Défis Opti-Math
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à

Défis Opti-Math – Solutions
Solutions des questions du Défi Opti-Math. Un défi mathématique pour tous les élèves du secondaire.

