- 2 minutes de lecture
Un défi mathématique pour tous les élèves du secondaire
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à encourager la pratique de la résolution de problèmes dans un esprit ludique et à démysti- fier, auprès des jeunes, les modes de pensée qui caractérisent la mathématique.
Voici des questions qui ont été sélectionnées parmi d’anciennes questions des Concours Opti-Math et Opti-Math+ du GRMS.
Opti-Math 2011
Situation 12 – Le triangle et le parallélogramme
Un point M se déplace sur la base AD d’un parallélogramme.
En se déplaçant, le point M entraîne la formation d’un triangle ABM et d’un parallélogramme MECD
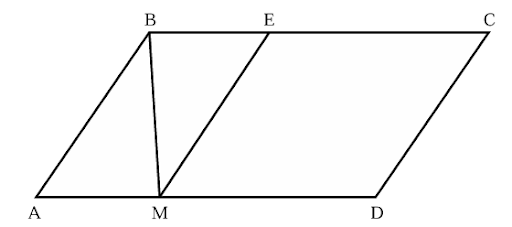
La base AD mesure 12 cm.
Détermine la position du point M sur AD lorsque l’aire du triangle ABM est le double de celle du parallélogramme MECD.
Opti-Math 2013
Situation 7 – Les nombres chanceux
Il les nomma « nombres chanceux » en lien avec un récit de l’historien Flavius Josèphe. Ce dernier raconte que, lors de la première guerre judéo-romaine, il s’est retrouvé coincé avec 40 de ses compagnons dans une situation dont la seule issue possible était la mort. Il proposa un stratagème qui éliminerait un combattant sur trois jusqu’à ce qu’il n’en reste qu’un avec lui.
- le premier terme de la suite des nombres chanceux est 1 et on supprime un nombre sur 2, soit 2, 4, 6, 8…;
- le premier nombre qui reste est 3 et on supprime ensuite un nombre sur 3, soit 5, 11, 17…;
- le premier nombre qui reste est 7 et on élimine un nombre sur 7, soit 19, 39, 61…;
- et ainsi de suite …
- Quels sont les nombres chanceux inférieurs à 50. Selon Ulam, il semble que tout nombre pair soit la somme de deux nombres chanceux, identiques ou non.
- Trouve les deux nombres chanceux différents dont la somme est 54.
Opti-Math+ 1998
Situation 14 – L’aire de polygones
Des figures ayant le même périmètre n’ont pas nécessairement la même aire.
Que vaut l’aire du carré A si son périmètre est de 120 cm ?- Que vaut l’aire de l’hexagone régulier B si son périmètre est de 120 cm ? Arrondis la réponse à la dizaine près.
- Que vaut l’aire du pentagone régulier C si son périmètre est de 120 cm ? Arrondis la réponse à la dizaine près.
Que vaut l’aire du carré A si son périmètre est de 120 cm ?Opti-Math+ 2015
Situation 9 – Quand est-ce qu’on arrive ?
Lors d’un voyage, Julie roule à une certaine vitesse.
- À partir de ces informations, calcule la durée du voyage de Julie.
- Une fois Julie rendue à destination, deux de ses amies viennent la rejoindre. Les deux ont la même distance à parcourir. La première roule à une vitesse moyenne de 90 km/h et la deuxième, à une vitesse moyenne de 95 km/h.Si elles arrivent à 15 minutes d’intervalle, combien de kilomètres ont-elles dû parcourir pour rejoindre Julie ?
Articles dans ce numéro
Mot de la Directrice
Il me fait plaisir de vous présenter votre tout nouveau numéro de la revue Envol, celui-ci regorgeant de plusieurs articles diversifiés et enrichissants qui sauront très certainement vous inspirer…
Le GRMS : Alimenter la réflexion
Je suis heureux de vous présenter ce nouveau numéro de notre revue, un moment privilégié pour revenir sur notre dernier congrès et jeter un œil vers l’avenir…
Hommage à Pierre Couillard, plus qu’un « brancheux » de fils
Son entrée dans le monde de l’éducation, à la fin des années 1980, où les TRS 80 de la compagnie Tandy entraient dans les écoles, n’était pas calculée par Pierre..
La classe collabo-réflexive en mathématiques : un bref survol
Une classe collabo-réflexive se distingue par son dynamisme : les élèves, debout et répartis dans la salle, travaillent en équipe sur des surfaces verticales non permanentes.
La partie entière, tranchée mince : une approche BTC en action
Ce chapitre explique comment maintenir l’intérêt des élèves grâce au « thin slicing », illustré par un exemple sur la factorisation des trinômes de la forme…
Desmos Mode Examen : un outil équitable pour soutenir l’évaluation en mathématique et favoriser la réussite
Parmi les outils numériques disponibles, la calculatrice graphique de Desmos s’est rapidement imposée comme une ressource pédagogique de premier plan.
Évaluer autrement: tâche flexible, créative et colorée en mathématiques CST et TS de cinquième secondaire
Probablement comme plusieurs d’entre vous, nous trouvons important de présenter à nos élèves des tâches diversifiées et stimulantes pour favoriser leur engagement et leur motivation
Parole aux communautés de pratique interordres secondaire-collégial en mathématiques
Comment faciliter la transition secondaire-collégial en mathématiques des élèves finissants de 5e secondaire qui feront leur entrée dans le programme Sciences de la nature au cégep ?
Leçons de la classe de mathématiques
L’après-midi bat son plein et les élèves travaillent fort à résoudre les tâches que je leur propose sur le pourcentage en contexte de calcul mental. …
Un codage à la Gödel
Le but de ce court texte est de partager une idée avec laquelle j’avais jonglé lors du printemps 2022, puis mise à l’essai au cours de l’année scolaire qui a suivi. . …
La manipulation au secondaire : est-ce vraiment nécessaire ?
Lors du dernier congrès du GRMS, Geneviève Dupuis, conseillère pédagogique du Récit de l’enseignement privé, et moi-même avons donné un atelier en mode hybride..
5e article: la marche aléatoire (probabilltés)
Récit #5 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Marche aléatoire
Défis Opti-Math
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à encourager la pratique de la résolution de problèmes dans…
Défis Opti-Math – Solutions
Solutions des questions du Défi Opti-Math. Un défi mathématique pour tous les élèves du secondaire.
