Revue l'Envol • Défis Opti-Math

Solutions des questions

Opti-Math 2011
Situation 12 – Le triangle et le parallélogramme

Distance de A à M: x

Distance de M à D: 12 – x

Hauteur: h

Aire du triangle ABM: $ \frac{hx}{2} $

Aire du parallélogramme MEC: h (12 – x)

On cherche la valeur de x lorsque: $ \frac{hx}{2} $ = 2h(12 – x)

En divisant chaque membre par h, on obtient que:

$ \frac{x}{2} $ = 2(12 – x)
$ \frac{x}{2} $ = 24 – 2x
x = 2(24 – 2x)
x = 48 – 4x
x + 4x = 48
5x = 48
x = 9,6

Donc, le point M doit être à 9,6 cm du point A.

Opti-Math+ 1998
Situation 14 – L’aire de polygones

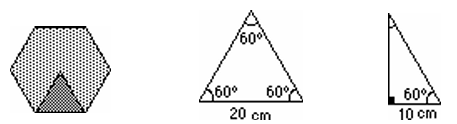
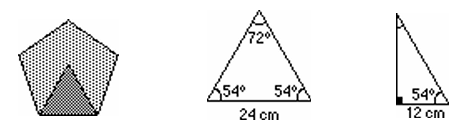
Si le périmètre du carré A est de 120 cm, la mesure de chaque côté est de 30 cm. L’aire du carré A est donc de 900 cm².
Si le périmètre de l’hexagone régulier B est de 120 cm, chaque côté mesure 20 cm. L’hexagone régulier B contient six triangles équilatéraux. La base de chacun des triangles mesure 20 cm. Chaque triangle équilatéral contient deux triangles rectangles, dont l’un des angles mesure 60°. La base du triangle rectangle mesure 10 cm.

La hauteur du triangle rectangle mesure 17,320508 cm. L’aire du triangle isocèle mesure 173,20508 cm². L’aire de l’hexagone régulier B mesure 1039,2305 cm². Arrondi à la dizaine près, on a 1040 cm².
Si le périmètre du pentagone régulier C est de 120 cm, chaque côté mesure 24 cm. Le pentagone régulier C contient cinq triangles isocèles dont l’angle au sommet mesure 72° et dont les angles isométriques à la base mesurent 54°. La base de chacun des triangles mesure 24 cm. Chaque triangle isocèle contient deux triangles rectangles dont l’un des angles mesure 54°. La base du triangle rectangle mesure 12 cm.

La hauteur du triangle rectangle mesure 16,516583 cm. L’aire du triangle isocèle mesure 198,199 cm². L’aire du pentagone régulier C mesure 990,99498 cm². Arrondi à la dizaine près, on a 990 cm².

Opti-Math 2013
Situation 7 – Les nombres chanceux

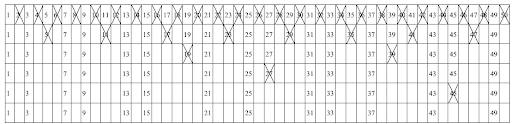
En résumé, de la suite des nombres naturels jusqu’à 50 de la première ligne, on élimine un entier sur deux, soient les nombres pairs.

Dans la deuxième ligne, on élimine un entier sur trois, car le nombre chanceux suivant est 3, soient les nombres 5, 11, 17, 23, 29, 35, 41 et 47.

Dans la troisième ligne, on élimine un entier sur sept, car le nombre chanceux suivant est 7, soient les nombres 19 et 39.

Dans la quatrième ligne, on élimine un entier sur neuf, car le nombre chanceux suivant est 9, soit le nombre 27.

Finalement, dans la cinquième ligne, on élimine un entier sur 13, car le nombre chanceux suivant est 13, soit le nombre 45 .

Par la suite, il devient inutile de continuer, car les nombres à éliminer sont tous plus grands que 50. Dans cette suite, il ne reste que les nombres chanceux.

L’ensemble des nombres chanceux inférieurs à 50 est :
{1; 3; 7; 9; 13; 15; 21; 25; 31; 33; 37; 43; 49}
Par essais et erreurs, on déduit que les deux seuls nombres chanceux différents, dont la somme est 54, sont 21 et 33.

Opti-Math+ 2015 Situation 9 – Quand est-ce qu’on arrive?

a) Posons v, la vitesse moyenne de la voiture.

La vitesse moyenne, augmentée de 5 %, est 1,05v et celle diminuée de 10% est 0,9v.

On peut donc poser les deux équations suivantes:

y₁ = 1,05v(t – 18)
y₂ = 0,9v(t + 42)

où t est le temps écoulé, en minutes, et y, la distance parcourue, en kilomètres.

On résout le système d’équations par la méthode de comparaison :

1,05v(t – 18) = 0,9v(t + 42)
1,05(t – 18) = 0,9(t + 42)
t = 378

La durée du voyage de Julie est de 378 minutes.

b) Posons :

x : le temps écoulé, en heures;
y₃ : la distance parcourue, en kilomètres, par la première amie ;
y₄ : la distance parcourue, en kilomètres, par la deuxième amie.

On peut donc poser les deux équations suivantes:

y₃ = 90(x + 0,25)
y₄ = 95x

On résout le système d’équations par la méthode de comparaison:

90(x + 0,25) = 95x
90x + 22,5 = 95x
22,5 = 5x
4,5=x

On remplace la valeur de x dans l’une des deux équations:

y₄ = 95x
y₄ = 95×4,5
y₄ = 427,5

Elles ont dû parcourir 427,5 km pour rejoindre Julie.

Vos prix
d’excellence

300$

Prix Richard Pallascio

Prix 2023 : Bravo à Bénédicte Ferragne-Simard, Achraf Hajby, Fouzia Jetto, Anne-Marie Lagueux et Loula Abdourahim pour leur contribution à la revue Envol avec leur article L’apprentissage des maths PAR la résolution de problème. Ils remportent le prix Richard Pallascio et la bourse de 300 $.

Description : Prix pour les auteurs de la revue.

Modalités : Un jury nommé par le conseil d’administration du GRMS déterminera l’article primé et fera connaître son choix lors de la session de perfectionnement du GRMS.

Critères d’admissibilité

Article original selon le jugement du jury;
Ne pas être membre du conseil d’administration du GRMS;
Avoir publié un article original dans la revue Envol avant le 30 juin.

Il doit s’agir d’un article n’ayant pas été puisé à une autre source, ou simplement traduit. Il peut cependant s’agir d’un article basé sur un écrit d’une autre source à la condition que cette source soit citée et qu’un apport original et personnel de l’auteur soit jugé pertinent par le jury.

Montant accordé : 300 $

Note : Si l’article est présenté par une équipe, le montant du prix sera partagé entre les membres de l’équipe.

Prix Emma-Castelnuovo

Prix 2023 :

Bravo à nos lauréats 2023 :

Vicky Nadeau – UdeS
Camille Lefebvre – ULaval
Alexandre Alie – UQAM
Florence Lavallée – UQTR
Chloé Bénard – UQAR
Anne-Marie Auclair – UQAC
Rosalie Bédard – UQO
Jonathan Morcos – UdeM

Description : Prix remis à neuf diplômés (es) (une personne par université participante) dans le programme d’enseignement des mathématiques au secondaire.

Critères d’admissibilité: Être bachelier dans le programme d’enseignement des mathématiques au secondaire dans une des neuf universités participantes.

Ce prix est conjointement offert par le Groupe des responsables en mathé- matique au secondaire (GRMS) et l’Association mathématique du Québec (AMQ). En accord avec les neuf universités québécoises francophones, ce prix sera remis à l’étudiant(e) diplômé(e) qui se démarque le plus de sa cohorte dans chacune des universités participantes.

Les universités sont : Université de Sherbrooke, Université de Montréal, Université Laval, Université du Québec à Trois-Rivières, Université du Québec à Montréal, Université du Québec en Outaouais, Université
du Québec à Chicoutimi, Université du Québec à Rimouski et Université du Québec en Abitibi-Témiscamingue.

Le prix : Une médaille d’honneur ainsi qu’une adhésion à l’association (GRMS) seront remises aux titulaires de ce prix.

Participez
c'est pour vous!!

Prix FERMAT

300$

Prix 2023 : Bravo à Jean-François Blanchet pour sa contri- bution exceptionnelle à l’avancement de la mathématique qui se mérite le prix Claude Janvier et la bourse de 500 $.

Vous désirez souligner le travail d’un de vos pairs ?

Description : Prix d’excellence Claude Janvier remis annuellement à un enseignant(e) s’étant démarqué(e) dans son milieu par son dynamisme, son leadership, son innovation, la qualité de son enseignement ou son rayonnement.

Critères d’admissibilité: La candidate ou le candidat doit :

être membre en règle du GRMS;
ne pas être membre du conseil d’administration du GRMS;
avoir œuvré dans le domaine de l’enseignement de la mathématique au secondaire.

Montant accordé :

Maximum de 300$ peuvent être accordé selon l’étendue du projet;
Il est possible que plusieurs projets différents soient retenus et que le prix soit remis à plusieurs récipiendaires au prorata des projets présentés.

Attribution du prix : Le conseil d’administration du GRMS se réunira une fois l’an en juin pour attribuer le prix à la personne méritante. Vous désirez souligner le travail d’un de vos pairs ? Envoyez aux membres du conseil d’administration une brève description expliquant votre recommandation à l’adresse secretariat@grms.qc.ca.

Formule
simplifiée

Prix Claude
Janvier

500$

Prix 2023 : Bravo à Marika Perrault pour avoir oser faire des maths en plein air et qui se mérite le prix Fermat et une somme de 300$.

Vous avez besoin d’ $ $ $ pour un projet ?
Vos budgets sont coupés ? on peut vous aider !

Description : Prix pour le meilleur scénario d’enseignement (1er cycle ou 2e cycle du secondaire)

Critères d’admissibilité

être membre en règle du GRMS ;
ne pas être membre du conseil d’administration du GRMS ;
avoir une bonne idée pour la réalisation d’un projet,
mais ne pas avoir le soutien financier pour le réaliser ;
brève description du projet et de la clientèle visée ;
permettre la publication du projet dans la revue Envol.

Montant accordé :

Maximum de 300$ peuvent être accordé selon l’étendue du projet;
Il est possible que plusieurs projets différents soient retenus et que le prix soit remis à plusieurs récipiendaires au prorata des projets présentés.

Note : Si le projet est présenté par une équipe, le montant du prix sera partagé entre les membres de l’équipe.

Attribution du prix : Le conseil d’administration du GRMS se
réunira une fois l’an en juin pour attribuer le prix à la ou les personnes méritantes. Vous désirez présenter votre projet ? Envoyez aux membres du conseil d’administration une brève description de celui-ci à l’adresse secretariat@grms.qc.ca.

Revue Envol

Revue Envol