Évaluer autrement:
tâche flexible, créative et colorée en mathématiques CST et TS de cinquième secondaire
- 10 minutes de lecture
Isabelle Gamache
Enseignante de mathématiques, école secondaire Bon-Pasteur
Audrey Richard
Enseignante de mathématiques, école secondaire Bon-Pasteur
Probablement comme plusieurs d’entre vous, nous trouvons important de présenter à nos élèves des tâches diversifiées et stimulantes pour favoriser leur engagement et leur motivation, et ce, tout au long de l’année scolaire. Ils peuvent ainsi s’approprier les nombreuses connaissances du programme de mathématiques tout en développant leurs compétences par la réalisation de projets ou d’activités. Nous avions cependant une réflexion sur le fait que nous les contraignions malgré tout à faire une évaluation dite plus traditionnelle en fin d’année. Nous cherchions donc une tâche créative qui soit récapitulative, flexible et pouvant être évaluée à l’aide de la triangulation. De plus, nous souhaitions l’adapter à nos séquences d’enseignement respectives. Nous avons donc créé une tâche qui répondait à nos besoins de faire les choses autrement, même en fin d’année scolaire.
Nous vous présentons donc cette tâche, divisée en sept parties. Il est important de prendre note qu’il n’est pas obligatoire de faire l’entièreté de la tâche et qu’il est possible de la fragmenter tout au long de l’année au lieu de la faire entièrement à la fin de l’année. Sa flexibilité vous permet de l’organiser à votre guise, selon vos réalités et vos besoins. Vous pouvez donner un cahier intégral de la tâche à l’élève ou adapter celui-ci pour une tâche fragmentée. De plus, même si vous n’avez pas accès au matériel numérique suggéré, il est aussi possible de faire la tâche.
Voici le lien pour accéder à l’ensemble des documents lié à cette tâche : GRMS 2024 Jeu de Trouble (5e secondaire)
La tâche :
Construction d’une planche de jeu ( inspirée du jeu Trouble ©)
Partie 1 : Le logo
Temps suggéré : 300 minutes
Matériel
- Cahier de la tâche
- Ordinateur et application Desmos
- Machine de découpe vinyle (facultatif)
- Vinyle imprimable autocollant (facultatif)
Nous faisions déjà réaliser une tâche de dessin avec l’application Desmos. Nous avons donc décidé de l’intégrer dans notre projet. Selon la séquence d’enseignement, l’élève doit créer le logo de son jeu tout en respectant les contraintes qui lui sont données.
Contraintes pour CST
- Le logo est situé dans les 4 quadrants du plan cartésien ;
- Il doit y avoir au moins 12 polygones de contraintes ;
- Au moins huit droites doivent avoir une pente différente de 0, 1, ou -1 ;
- Un des polygones de contraintes doit avoir un sommet au point (4,6) ;
- Les points (1,1) et (2,-2) doivent être des solutions d’un même polygone de contraintes.
Contraintes pour TS
- Le logo est situé dans les 4 quadrants du plan cartésien;
- Le logo doit être formé d’au moins 5 types de fonctions différentes;
- Le logo doit contenir au moins 2 coniques différentes;
- Le logo doit contenir au moins 4 inéquations.
La totalité de cette partie se retrouve intégrée dans une activité Desmos dont voici les liens pour chacune des séquences de mathématiques :
Figures 3 et 4 Élèves réalisant la tâche de dessin du logo
Lorsque son dessin du logo est terminé, l’élève peut importer celui-ci dans le logiciel d’une machine de découpe vinyle (Cricut ou Silhouette). On utilise le procédé « print and cut » pour l’impression et la découpe du logo. Il est possible d’utiliser un papier vinyle autocollant ou tout simplement du papier afin que l’élève puisse le coller sur son jeu.
Partie 2 : Les maisons
Temps suggéré : 75 minutes
Matériel
- Cahier de la tâche
- Machine de découpe vinyle (facultatif)
- Vinyle autocollant permanent de 4 couleurs différentes (facultatif)
Sur la planche de jeu, les maisons sont les endroits où les pions sont placés au début du jeu (figure 5) . Chaque joueur a sa maison et ses pions sont de la même couleur que celle-ci. Les quatre maisons ont aussi la même forme géométrique. Dans cette partie de la tâche, l’élève doit déterminer la forme et la grandeur d’une maison. Pour ce faire, il doit respecter certaines contraintes présentées dans le cahier de la tâche et il a recours aux notions de figures équivalentes et d’optimisation.
Une fois la forme et les dimensions d’une maison établies, l’élève utilise à nouveau le logiciel de la machine de découpe pour les dessiner et les découper. Il est suggéré d’utiliser du vinyle permanent, de quatre couleurs différentes.
Partie 3 : Les pions
Temps suggéré : 150 minutes (excluant l’impression 3D)
Matériel
- Cahier de la tâche
- Application Tinkercad (ou toute autre application de dessin 3D)
- Application Geogebra
- Imprimante 3D (facultatif)
- Filament de 4 couleurs agencées à celles du vinyle
La partie de la confection des pions requiert la notion de solides équivalents et le choix du pion fait appel aux procédures de vote pour l’élève de CST. Pour l’élève de la séquence TS, il a le libre choix de son modèle.
Contraintes géométriques à respecter
- Le nouveau pion doit avoir la même hauteur que le pion original;
- Les quatre pions doivent pouvoir se retrouver simultanément dans l’espace délimité de la maison;
- L’un des solides composant le pion doit être équivalent au cône tronqué du pion initial, avec un maximum de 2 % d’écart.
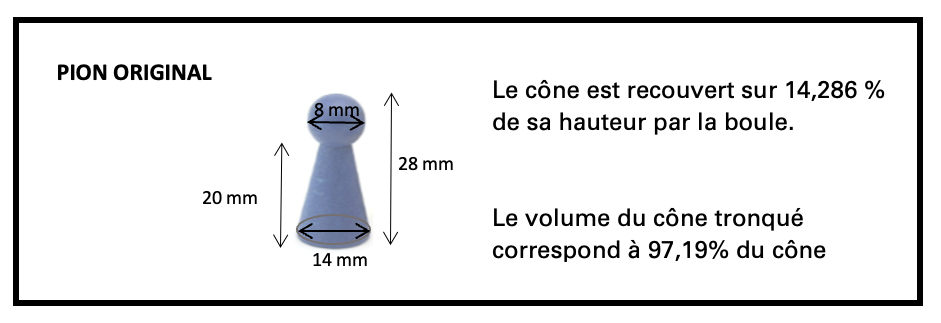
Dans cette partie, l’élève a des choix à faire. Le dessin du pion peut varier d’un élève à l’autre, que ce soit par ses dimensions (CST-TS) ou par sa forme (TS). Après avoir fait les calculs nécessaires, l’élève doit dessiner le pion dans l’application de dessin 3D Tinkercad. Il peut ensuite procéder à l’impression 3D de tous ses pions. Il faut imprimer quatre pions pour chacune des quatre couleurs du jeu, ce qui fait 16 pions par élève (ou équipe).
Figures 8 et 9 Exemples de pions
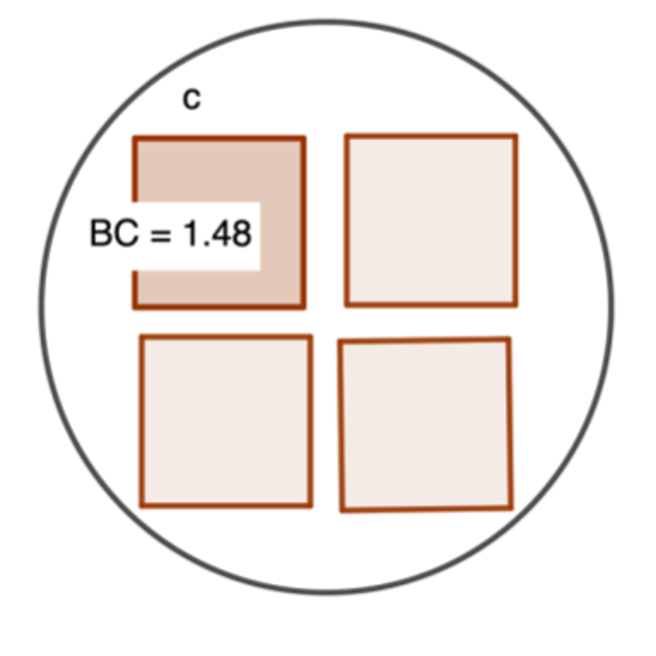
L’élève doit aussi fournir une preuve géométrique (figure 10) que quatre pions entrent en même temps dans la maison (nous suggérons l’utilisation de Geogebra).
Partie 4 : Le dé
Temps suggéré : 75 minutes (excluant l’impression 3D)
Matériel:
- Cahier de la tâche
- Application Tinkercad (ou toute autre application dessin 3D)
- Imprimante 3D (facultatif)
- Filament blanc ou noir (ou d’une couleur différente de celles des pions) (facultatif)
Cette étape est très simple au niveau des calculs à effectuer, mais plus difficile techniquement pour le dessin 3D. Les élèves doivent déterminer les dimensions du dé sachant son volume. Ils doivent le dessiner à l’aide de Tinkercad. Sur chaque face du dé, ils doivent insérer un chiffre de 1 à 6 (ou des points pour désigner les chiffres). Ensuite, ils procèdent à l’impression 3D.
Partie 5 : Le boîtier de rangement des pions et du dé
Temps suggéré : 30 minutes (excluant l’impression 3D)
Matériel:
- Cahier de la tâche
- Imprimante 3D (facultatif)
- Filament de la couleur de votre choix
Nous voulions que les élèves aient un boîtier pour ranger les pions et le dé. Une fois de plus, nous faisons appel aux notions géométriques pour cette partie. Le schéma d’un solide décomposable avec ses mesures est fourni à l’élève dans le cahier de la tâche. On lui présente également quatre choix de boîtiers. Il doit choisir celui qui est équivalent au solide décomposable. Ensuite, nous lui remettons le fichier STL du boîtier choisi afin qu’il puisse procéder à son impression.
Partie 6 : Les cases de déplacement et de lieu sûr
Temps suggéré : 30 minutes
Matériel:
- Cahier de la tâche
- Machine de découpe vinyle (facultatif)
- Vinyle autocollant permanent de 4 couleurs différentes (facultatif)
- Vinyle autocollant permanent blanc ou noir (facultatif)
Chaque case du jeu doit être identique à la base du pion choisi, de forme carrée ou circulaire. Il peut donc y avoir des cases de jeu différentes pour chaque élève ou équipe. L’impression des cinq figures pour chacune des quatre couleurs du jeu peut se faire à l’aide de la découpe vinyle. Il s’agit des cases de lieu sûr. Il faut également découper 36 figures blanches ou noires (au choix de l’élève) pour les cases de déplacement. On termine cette étape en dessinant et en découpant une flèche pour chacune des quatre couleurs du jeu afin d’indiquer sur la planche le sens des déplacements.
Partie 7 : Le montage de la planche de jeu
Temps suggéré : 30 minutes
Matériel:
- Planche de bois de 25,5 cm x 25,5 cm
Cette partie n’a rien de mathématique. Il s’agit de prendre le temps de tout coller sur la planche de jeu en suivant les étapes fournies dans les documents de la tâche.
Figures 14 et 15 Montage final de la planche de jeu
Observations et évaluation
Chaque partie répond à des cibles d’apprentissage précises et chaque cible est évaluée soit par des observations, par des conversations ou par une production. Il est important de planifier cette évaluation avant de donner la tâche aux élèves.
Les traces sont consignées dans un tableur. Notre outil de consignation et notre outil de correction sont deux tableurs Excel. L’outil de correction a été programmé afin de faciliter la tâche de correction puisqu’il s’adapte aux différents résultats obtenus par l’élève.
Conclusion
Ce projet créatif permet aux élèves d’en apprendre davantage sur certaines applications telles que Tinkercad, Geogebra, Desmos et les applications associées à l’imprimante 3D et à la découpe vinyle. Cela leur permet donc d’atteindre les cibles de la progression des apprentissages TIC. Nous suggérons de faire vivre ce projet en équipe, puisqu’il permet aux élèves de travailler en collaboration, selon leurs différentes forces et habiletés. De plus, cela permet de limiter le nombre de pièces de jeu à imprimer. En effet, dans une même équipe, il est possible d’avoir des experts en dessin 3D, en informatique et en organisation. Les jeunes peuvent ensuite repartir avec leur création, avec quelque chose de tangible. Ils sont motivés par la tâche à faire et fiers de ce qu’ils réalisent, ce qui permet un réel engagement dans leur apprentissage.
Articles dans ce numéro
Mot de la Directrice
Il me fait plaisir de vous présenter votre tout nouveau numéro de la revue Envol, celui-ci regorgeant de plusieurs articles diversifiés et enrichissants qui sauront très certainement vous inspirer…
Le GRMS : Alimenter la réflexion
Je suis heureux de vous présenter ce nouveau numéro de notre revue, un moment privilégié pour revenir sur notre dernier congrès et jeter un œil vers l’avenir…
Hommage à Pierre Couillard, plus qu’un « brancheux » de fils
Son entrée dans le monde de l’éducation, à la fin des années 1980, où les TRS 80 de la compagnie Tandy entraient dans les écoles, n’était pas calculée par Pierre..
La classe collabo-réflexive en mathématiques : un bref survol
Une classe collabo-réflexive se distingue par son dynamisme : les élèves, debout et répartis dans la salle, travaillent en équipe sur des surfaces verticales non permanentes.
La partie entière, tranchée mince : une approche BTC en action
Ce chapitre explique comment maintenir l’intérêt des élèves grâce au « thin slicing », illustré par un exemple sur la factorisation des trinômes de la forme…
Desmos Mode Examen : un outil équitable pour soutenir l’évaluation en mathématique et favoriser la réussite
Parmi les outils numériques disponibles, la calculatrice graphique de Desmos s’est rapidement imposée comme une ressource pédagogique de premier plan.
Évaluer autrement: tâche flexible, créative et colorée en mathématiques CST et TS de cinquième secondaire
Probablement comme plusieurs d’entre vous, nous trouvons important de présenter à nos élèves des tâches diversifiées et stimulantes pour favoriser leur engagement et leur motivation
Parole aux communautés de pratique interordres secondaire-collégial en mathématiques
Comment faciliter la transition secondaire-collégial en mathématiques des élèves finissants de 5e secondaire qui feront leur entrée dans le programme Sciences de la nature au cégep ?
Leçons de la classe de mathématiques
L’après-midi bat son plein et les élèves travaillent fort à résoudre les tâches que je leur propose sur le pourcentage en contexte de calcul mental. …
Un codage à la Gödel
Le but de ce court texte est de partager une idée avec laquelle j’avais jonglé lors du printemps 2022, puis mise à l’essai au cours de l’année scolaire qui a suivi. . …
