Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

La classe collabo-réflexive
en mathématiques:
un bref survol

  • 7 minutes de lecture
Picture of Frédéric Ouellet

Frédéric Ouellet

  • Consultant en mathématique et pédagogie numérique
  • Directeur des services pédagogiques au Collège de Sainte-Anne-de-la-Pocatière
    Ancien président du GRMS
  • fredouellet76@gmail.com

Oyé ! Oyé ! Enseignants de mathématiques, prenez un moment pour noter un événement à ne pas manquer : Peter Liljedahl sera présent au congrès du GRMS, les 5 et 6 novembre 2025, à Sherbrooke. Si ce nom ne vous est pas familier, sachez qu’il est à l’origine de l’approche de la classe collabo-réflexive, une méthode qui engage activement les élèves en mathématiques.

Une classe collabo-réflexive se distingue par son dynamisme : les élèves, debout et répartis dans la salle, travaillent en équipe sur des surfaces verticales non permanentes. Cette approche favorise l’engagement, la réflexion collective et la mise en valeur du raisonnement des élèves. L’enseignant, plutôt que de dispenser un savoir magistral, guide la réflexion à travers des questions stratégiques, plaçant ainsi les élèves au cœur de leur apprentissage.

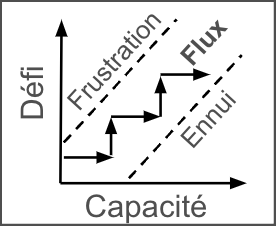Traditionnellement, les mathématiques sont souvent perçues comme une discipline centrée sur l’apprentissage de formules et d’algorithmes appliqués à des exercices. Mais cette vision réductrice ne reflète pas tout le potentiel des mathématiques ! La classe collabo-réflexive propose une alternative où la résolution de problèmes devient une occasion de réfléchir, d’argumenter et de partager ses idées. L’objectif étant de garder l’élève dans la zone de flux, cette zone située entre la frustration et l’ennui !

Les pratiques pédagogiques d’une classe collabo-réflexive en mathématiques

Développée à partir de recherches menées par Peter Liljedahl à l’Université Simon Fraser de Vancouver, cette approche repose sur 14 pratiques pédagogiques à haut rendement.

  1. Proposer des problèmes réflexifs
  2. Former des équipes visiblement aléatoires à une fréquence régulière
  3. Utiliser des surfaces verticales non permanentes (SVNP)
  4. Remodeler la classe
  5. Répondre uniquement aux questions réflexives
  6. Proposer un problème réflexif dans les premières minutes du cours, à l’oral, alors que les élèves sont debout
  7. Poser des questions de vérification de la compréhension
  8. Mobiliser les connaissances
  9. Utiliser des indices et des intensifications de manière asynchrone pour maintenir le flux
  10. Consolider à partir de la base
  11. Demander aux élèves d’écrire des notes significatives
  12. Évaluer ce que l’on valorise
  13. Aider les élèves à voir où ils en sont et où ils s’en vont
  14. Évaluer en fonction des données (et non des points)

Pour vous rassurer, vous n’avez pas besoin de mettre en application l’ensemble de ces 14 pratiques pédagogiques afin de vous lancer dans le principe de la classe collabo-réflexive. Cependant, certaines sont essentielles et doivent être mises en place en respectant une certaine séquence.

La base d’une classe collabo-réflexive repose sur les trois premières pratiques, soit proposer à nos élèves des problèmes réflexifs qu’ils travailleront en équipes visiblement aléatoires sur des surfaces verticales non permanentes (SVNP). L’application conjointe de ces trois pratiques transforme la dynamique de classe et crée un environnement propice à la collaboration et à la réflexion mathématique.

Pour débuter avec la classe collabo-réflexive en mathématiques

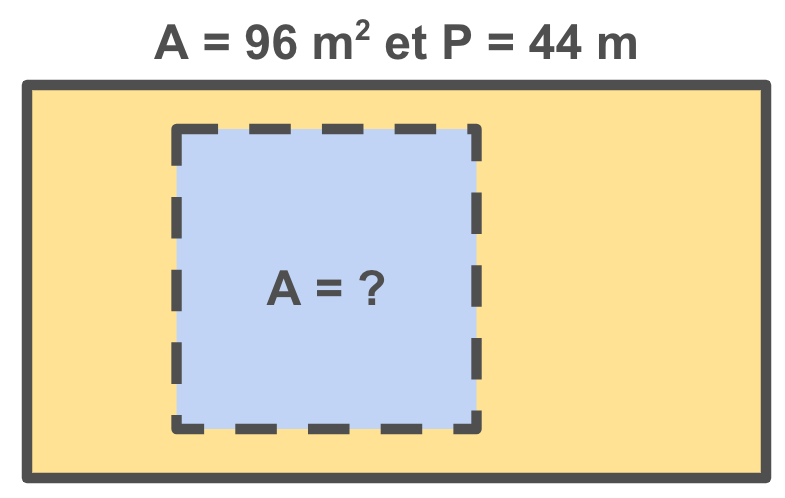Pour réfléchir, l’élève doit être placé en contexte où la réflexion est possible. Pour ce faire, il faut donner à nos élèves des problèmes réflexifs qui pourront être reliés ou non à notre programme d’étude. Par exemple, on peut donner à nos élèves le problème suivant: Un rectangle a une aire de 96 m2 et un périmètre de 44 m. Quelle est l’aire du plus grand carré que l’on peut dessiner à l’intérieur de ce rectangle?

Ce problème ne nécessite que des notions de première secondaire afin de le résoudre, mais pourrait être adapté ou même utilisé tel quel à plusieurs niveaux du secondaire.

Pour favoriser la collaboration entre les élèves, il est essentiel de mettre en place des conditions propices au travail d’équipe. Idéalement, la formation des équipes devrait se faire de manière aléatoire afin que les élèves s’habituent à interagir et coopérer avec l’ensemble de la classe. Une méthode simple consiste à distribuer une carte à jouer à chaque élève dès leur arrivée. Les élèves se regroupent ensuite en fonction de la valeur de leur carte : les as ensemble, les 2 ensemble, et ainsi de suite. Avant l’activité, prévoyez des emplacements spécifiques pour chaque équipe. L’idéal est de former des groupes de trois élèves. Si cela n’est pas possible, veillez à ne pas dépasser quatre élèves par équipe.

Les élèves analyseront donc le problème réflexif au sein de leur équipe formée aléatoirement. Pour rendre leur raisonnement visible, il suffit de leur fournir une SVNP par trio, clairement identifiée à leur équipe pour faciliter l’organisation dès le début de l’activité. En limitant chaque équipe à un seul crayon, on favorise la collaboration et la réflexion collective. Le rôle de l’enseignant sera alors de circuler parmi les équipes, de stimuler la réflexion et de minimiser ses interventions. Encouragez les élèves à observer les SVNP des autres équipes afin de trouver par eux-mêmes des réponses à leurs questionnements.

Approfondir la classe collabo-réflexive en mathématiques

Lorsque le premier groupe de pratiques pédagogiques (proposer des problèmes réflexifs, former des équipes aléatoires et utiliser des surfaces verticales non permanentes) sera bien ancré dans votre classe, vous pourrez alors expérimenter les autres pratiques dans cette séquence de groupements : 

  • Groupe 2 (pratiques pédagogiques 4, 5, 6, 7 et 8)
  • Groupe 3 (pratiques pédagogiques 9, 10 et 11)
  • Groupe 4 (pratiques pédagogiques 12, 13 et 14) 

Il s’agit sans doute d’un changement important, tant pour vous que pour vos élèves. Sans approfondir chaque pratique pédagogique en détail, retenons simplement que celles du groupe 2 impliquent que :

  • votre classe ne sera plus tournée vers l’avant
  • vous ne répondrez plus à toutes les questions posées dans la classe
  • vous poserez vos questions à l’oral alors que vos élèves seront debout autour de vous
  • vous les questionnerez régulièrement sur leur compréhension
  • vous les inciterez à aller voir les démarches des autres équipes de la classe. 

Pour les pratiques pédagogiques du groupe 3, vous aurez préparé des questions supplémentaires pour approfondir le problème réflexif. Vous veillerez à ce que les concepts de base soient bien compris avant de poursuivre et encouragerez vos élèves à prendre des notes en fonction de ce qu’ils jugent significatif pour eux, plutôt que pour vous.

Dans le groupe 4, l’accent sera mis sur l’évaluation de la compréhension des élèves dans la classe collabo-réflexive.

Ne vous inquiétez pas si vous n’adoptez pas toutes ces pratiques dès votre première année d’expérimentation. Prenez le temps de vous familiariser avec chacune d’elles à votre rythme. Grâce à l’approche collabo-réflexive, vous apprécierez de voir vos élèves réfléchir et s’engager activement dans leur apprentissage !

Envie d’en savoir plus et d’apprendre auprès d’un expert de la classe collabo-réflexive ? N’attendez plus ! Visitez le site du GRMS (www.grms.qc.ca) et inscrivez-vous au congrès !

À consulter

https://buildingthinkingclassrooms.com/

À lire

Building Thinking Classroom in Mathematics Ouvrage original (anglais) 

La classe collabo-réflexive en mathématiques Ouvrage adapté (français)

Partagez

Articles dans ce numéro

Se connecter