Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

La manipulation au secondaire:

est-ce vraiment
nécessaire ? 

  • 8 minutes de lecture
Picture of Mélanie Morissette

Mélanie Morissette

  • Conseillère à l’innovation pédagogique, Collège Saint-Alexandre de la Gatineau
  • Vice-présidente du GRMS
  • mmorissette@grms.qc.ca

Lors du dernier congrès du GRMS, Geneviève Dupuis, conseillère pédagogique du Récit de l’enseignement privé, et moi-même avons donné un atelier en mode hybride (présentiel et virtuel) intitulé « Manipuler au secondaire ? Mais pourquoi ? Et comment ? ». Avec plus de 100 participants, nous avons plongé dans l’univers de la manipulation en mathématique, cherchant à en comprendre ses avantages et à expérimenter cette approche pédagogique.

Tous les participants, qu’ils soient présents physiquement ou connectés à distance, ont eu l’opportunité de participer à des activités de manipulation et de collaborer avec des collègues. Les personnes présentes en salle avaient à leur disposition des objets de manipulation tangibles, ce qui leur a permis de rendre les concepts mathématiques plus visibles. Quant aux participants virtuels, les mêmes activités leur ont été présentées, mais de manière numérique. Ils ont eu accès à des simulations interactives et à des outils en ligne leur permettant de manipuler virtuellement les objets mathématiques.

L’objectif était de permettre à tous les participants de vivre pleinement l’expérience de manipulation afin de mieux comprendre cette approche pédagogique qui est essentielle, peu importe l’âge des apprenants. Les mathématiques, souvent perçues comme abstraites par de nombreux élèves, posent un défi important lorsqu’il s’agit de passer d’un concept théorique à une compréhension concrète. Ce transfert, souvent ardu, pousse certains élèves à mémoriser des méthodes en reproduisant les étapes de manière automatique, sans en comprendre le sens. Résultat : l’apprentissage devient superficiel et la rétention des savoirs s’effrite rapidement.

Combien de fois avons-nous eu l’impression de devoir enseigner de nouveau des notions déjà vues, comme si c’était la première fois que les élèves les rencontraient ? La manipulation intervient ici comme une solution intéressante. Elle offre une vision tangible des algorithmes, donne du sens aux notions et facilite l’assimilation à long terme. Une fois la compréhension acquise, les étapes plus mécaniques deviennent logiques, et l’élève peut non seulement apprendre, mais aussi ancrer ses connaissances de manière durable.

La représentation multimodale, qui combine explications verbales, symboles mathématiques, illustrations et objets concrets, renforce encore davantage la compréhension des élèves. Ce processus d’encodage par plusieurs canaux facilite la récupération de l’information en mémoire. De plus, au-delà de l’apprentissage, la manipulation agit comme un moteur de motivation. En explorant et en expérimentant les concepts mathématiques à l’aide d’objets, les élèves s’engagent plus activement. Les cours deviennent moins formels et plus stimulants.

Exemple d’un problème représenté de façon multimodale :

Marius a emprunté 12 $ à sa mère. Aujourd’hui, il est allé tondre le gazon chez son grand-père et il a gagné 15 $. Après avoir remboursé sa mère, combien d’argent lui reste-t-il ?

Représentation verbale : 

Marius a une dette de 12 $, ce qui représente -12 $.

Marius a gagné 15 $, ce qui représente + 15 $.

On cherche combien d’argent il lui reste après avoir payé sa dette.

Représentation avec illustrations : 

Représentation concrète : 

Représentation symbolique :

-12 + 15 = 3

Les défis de la manipulation en classe

Malgré ses avantages, la manipulation comporte son lot de défis pour les enseignants : le manque de temps, le coût des ressources, le besoin de matériel, l’espace d’entreposage, la gestion de classe, et l’absence d’activités prêtes à l’emploi. Pourtant, il est possible de surmonter ces obstacles. Dans les lignes qui suivent, je vous présenterai les activités vécues lors de notre atelier au GRMS.

Idées d’activités de manipulation

Voici quelques activités réalisables avec du matériel simple et facilement accessible. Si l’accès à ce matériel pose un problème, des solutions numériques peuvent venir à la rescousse.

    1. Les nombres entiers

      L’addition et la soustraction de nombres entiers posent souvent un défi, notamment la fameuse question : Pourquoi deux soustractions consécutives équivalent-elles à une addition ? Les jetons bicolores permettent d’illustrer ce raisonnement de manière visuelle et concrète. Nat Banting propose l’utilisation des « sceaux de zéros » pour rendre cet algorithme plus accessible. L’enseignant peut présenter des vidéos explicatives aux élèves, engager une discussion collective, puis les inviter à résoudre des équations à l’aide des jetons bicolores. Cette approche rend visible l’invisible, facilitant la compréhension de l’algorithme.
      Liens vers les activités :

    1. Les suites algébriques

Les suites algébriques offrent une transition naturelle vers l’algèbre. À l’aide de bâtons de popsicle, les élèves complètent des suites, ce qui leur permet d’observer des régularités et de formuler des généralisations .

      • En 1re  secondaire, cette activité introduit la notion de suite arithmétique ;
      • En 2e  secondaire, elle soutient la compréhension des expressions algébriques;
      • En 3e secondaire, elle devient un outil d’exploration des fonctions linéaires.

Les élèves doivent poursuivre des suites données avec des bâtons, puis chercher un modèle mathématique qui permet de généraliser la situation. Cette activité développe la pensée algébrique et la capacité de modélisation.

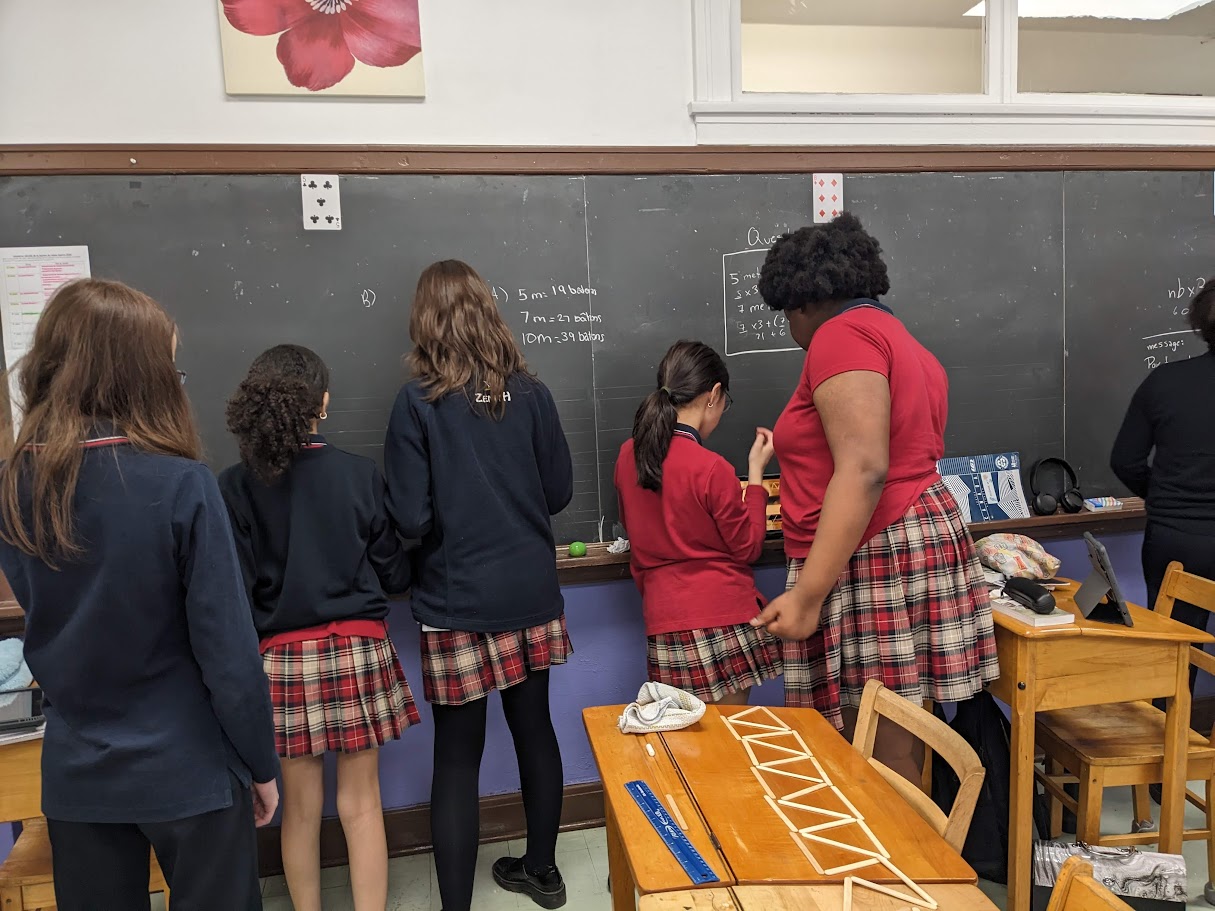
Lien vers le  activités :

Les problèmes « Open Middle », popularisés par Robert Kaplinsky, demandent aux élèves de compléter des cases vides dans des équations en utilisant très souvent les chiffres de 1 à 9, une seule fois chacun, de manière à obtenir un résultat vrai.

Lors du congrès, nous avons proposé une approche innovante pour résoudre des problèmes de type Open Middle : un Open Middle humain. Les participants, répartis en équipes de neuf, portaient des dossards numérotés de 1 à 9 et incarnaient les chiffres à déplacer dans les cases. Ils devaient se déplacer et changer de position afin de réajuster l’équation pour qu’elle soit juste. Cette activité dynamique et engageante a été un véritable coup de cœur pour les participants. Elle peut également être facilement adaptée pour l’extérieur, dans l’esprit des mathématiques en plein air, en dessinant les cases sur le sol à l’aide de craies.

Open Middle humain

Open Middle humain

Liens vers les activités :

    1. Discussions mathématiques

Les discussions mathématiques favorisent le développement du raisonnement logique, du sens des nombres, du vocabulaire, de la prise de risque, et bien plus encore. Dans cette activité, les élèves doivent déplacer deux cure-dents afin de former le plus grand nombre possible. Lors du partage en grand groupe, chaque élève expliquera les modifications apportées en utilisant un vocabulaire mathématique précis, notamment les termes associés à la valeur de position des nombres .

Lien vers le  activités :

 

Conclusion

Avec un matériel aussi simple que des jetons, des bâtons de popsicle, des cure-dents, du papier ou des craies, il est possible de proposer une multitude d’activités. La manipulation, souvent perçue comme un jeu par les élèves, permet de transformer des concepts abstraits en réalités tangibles. Elle agit comme un moteur de motivation, un outil de compréhension et un levier de rétention. Alors, n’hésitez pas à introduire des objets en classe et à encourager vos élèves à collaborer en équipe autour de ce matériel. Vous verrez rapidement l’impact sur leur engagement et leur compréhension des concepts.

Références :

Partagez

Articles dans ce numéro

Se connecter