Une approche BTC en action

Comme plusieurs d’entre vous, j’ai lu le livre de Peter Liljedahl, « Building Thinking Classroom », dit aussi BTC. Lorsque je voyais le mot « task », je le traduisais par « tâche » , que j’associe spontanément à des problèmes dits complexes. Suivez ce lien pour voir le genre de problème auquel je pense.  Cela m’amenait à en présenter un aux élèves de temps à autre, sans toujours prendre en compte l’approche graduelle suggérée dans le chapitre 9 du livre.  Ce chapitre explique comment maintenir l’intérêt des élèves grâce au « thin slicing », illustré par un exemple sur la factorisation des trinômes de la forme x2-Sx+P (p.151). J’avais sous-estimé l’importance de cette stratégie, ce qui était une erreur.

Découverte du « Thin Slicing »  en action

En mai dernier, j’ai eu la chance de participer au congrès de l’OAME et, plus particulièrement, à l’atelier «  Launch to Close », présenté par Peter Liljedahl lui-même. Cet atelier m’a permis d’approfondir ma compréhension de son livre en vivant une séquence d’enseignement sur les inéquations du premier degré. J’ai pu expérimenter une progression de « petits »  problèmes destinés à faire évoluer les conceptions et la compréhension des élèves. Chaque exercice, judicieusement choisi, permet aux élèves de développer des stratégies de résolution tout en raffinant leur maîtrise du concept. 

Une activité sur la partie entière, un exemple concret

Inspiré par cet atelier et une relecture du chapitre 9 du livre, j’ai commencé à imaginer comment transposer cette approche dans ma classe. Pourquoi ne pas l’utiliser pour introduire un nouveau concept, l’explorer tout au long d’un chapitre, voire même structurer une étape entière de cette façon?  

Au printemps dernier, j’ai demandé à mon stagiaire de lire le livre pour qu’il soit prêt dès la rentrée. Dès la première journée de classe, avec lui et notre conseiller pédagogique, nous avons conçu plusieurs séquences selon le modèle de classe collabo-réflexive pour la 3e secondaire et la 4e SN.  

Pour ma part, j’ai couvert les notions suivantes : manipulation d’expressions algébriques, factorisation, complétion de carré, passage de l’équation d’une parabole à son graphique, forme de la droite en géométrie analytique, inéquations à deux variables, et enfin, la partie entière. Les élèves ont ainsi découvert ou approfondi ces concepts par eux-même tout en collaborant.  

En toute modestie, je vous propose ici ma première activité sur la partie entière qui occupe une période de 70 minutes. Il est important de savoir qu’il s’agissait du premier contact des  élèves avec ce contenu.

Structure de la période

Une période est divisée en trois phases :

1. Réchauffement (5 minutes) : activation des connaissances préalables sans  préenseignement
2. Activité principale (40-45 minutes) : résolution de problèmes progressifs
3. Consolidation et prise de notes (20 minutes): retour sur les éléments vus pendant l’activité et formalisation  des apprentissages

Extraits du réchauffement vécu :

Enseignant: « Vous savez comment arrondir à l’unité ? » Élèves: « oui »

Enseignant:  «  3,2 ? »   Élèves: « 3 » 

Enseignant: «  3,6 ? » Élèves: « 4 »

Enseignant: «  Ça c’est arrondir  l’entier le plus près.
Mais qu’en est-il si je demande d’arrondir à l’entier inférieur?
Et si on notait cette opération d’arrondir à l’entier inférieur avec des crochets, comme cela  [5,45] ? »  Élèves: « 5 »      

Enseignant:  « Si nous avions [5,8] ? » Élèves: « 5 »     

Enseignant: « Que vaut [4,5]? » Élèves:  « 4  »    

Enseignant: « Et maintenant [-3,2 ]?  Élève 1: « -3» Élève 2: « -4 »

Enseignant: « Qu’en pensez vous ?  -3 ou -4 ? » 

La discussion avec les élèves a permis d’établir que ce sera  -4. 

Enseignant: « Ainsi, que sera [-2,9] ?   Élèves: « -3»

Cet échauffement prépare donc les élèves à la notion de partie entière sans introduire directement la fonction mathématique.

Les élèves en action, le développement de leur compréhension

L’activité principale, qui dure de 45 à 50 minutes (environ les deux tiers de la période), repose sur trois types de problèmes progressifs. Mon objectif est de les couvrir tous, chaque type s’appuyant sur les précédents avec de légères modifications. C’est à ce moment que je répartis les élèves en équipes aléatoires, travaillant sur des surfaces verticales. Le premier problème est [x]=8.  Je leur demande:  « Quelle est la plus petite valeur de x pour laquelle cette équation est vraie ? La plus grande ? D’autres valeurs possibles ?»  Les élèves recopient la question dans une section appelée bandeau, en haut de leur surface, réservée aux énoncés, et notent leurs réponses dans une  « banque  », une zone dédiée aux solutions pour leur permettre de conjecturer sur leurs observations.

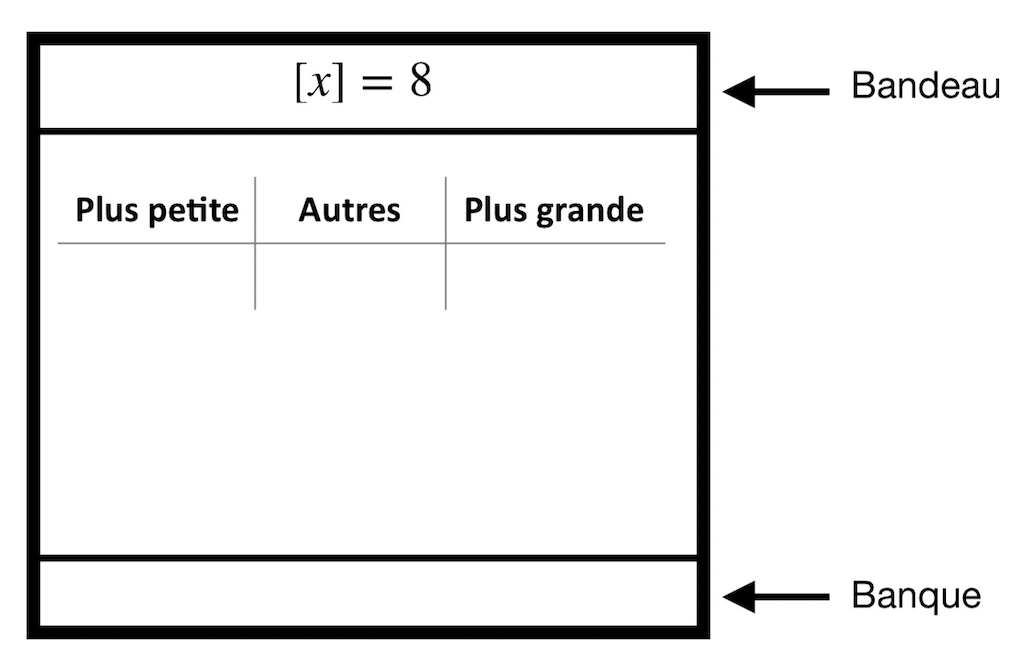
En circulant parmi les équipes, je leur demande de représenter leurs valeurs sur une droite numérique. Ce moment révèle parfois des lacunes : certains représentaient 8,999 au lieu d’utiliser 9 avec la notation du point ouvert  D’autres ont de la difficulté à représenter correctement les nombres négatifs.

Type 1 : Sans paramètre  « b » ou « h »

Enseignant : « Déterminer des valeurs de x possibles » 

Enseignant:   « Si tu avais à mettre ça sur une droite numérique? »

En écrivant la question dans le bandeau, les élèves peuvent prendre les questions des autres  équipes en regardant sur leur bandeau et résoudre les problèmes qu’ils n’ont pas encore faits. J’avais planifié trois exemples de type 1, mais je crois que deux exemples suffisent. Il est toutefois important de faire celui qui est négatif. 

Selon leur progression, j’introduis dans les différentes équipes les problèmes de type 2 où j’intègre un coefficient à l’intérieur de la partie entière. Ici, la section appelée la «  banque  » est importante. C’est l’endroit pour garder leurs réponses et remarquer le changement de longueur du palier.

Type 2 : Paramètre « b »,  longueur des paliers

Déjà, dans ce nouveau type de problème, quelques équipes abandonnent l’outil du petit tableau vu dans le type 1. 

Pour le troisième type de problème, j’introduis un coefficient négatif à l’intérieur de la partie entière. Le but est de leur faire observer l’inversion du sens des points pleins et vides.

Type  3 : Paramètre « b » négatif, le sens du palier

Certaines équipes n’atteignent pas tous les problèmes, mais la phase suivante permet de combler ces écarts.

Consolidation :

Pour les 20 dernières minutes, soit le tiers de la période, j’anime un retour structuré. Je commence par questionner les équipes moins avancées, passant des concepts simples aux plus complexes pour éviter les sauts de compréhension.

Enseignant:

« Qu’est-ce que vous avez remarqué? Écrivez sur votre surface verticale ce que vous devriez retenir. Faites le tour pour voir s’il vous manque des éléments. »

Élèves: 

« Il y a plusieurs valeurs possibles de x. »

« La longueur de l’intervalle varie. »

« Si le nombre est grand, la longueur de l’intervalle est petite. »

« La longueur est inversement proportionnelle au coefficient à l’intérieur. »

« L’ordre des points ouverts/fermés est inversé selon le signe du coefficient. »

Finalement, je propose d’autres exemples : 

Enseignant: «Lequel auriez-vous envie de faire en premier ?  Pourquoi ?  Ensuite lequel ? »

N’ayant pas eu le temps de compléter la consolidation, j’ai utilisé le modèle de Peter Liljedahl pour la prise de notes. Étant donné qu’il s’agissait de l’une de leurs premières fois, j’ai dirigé davantage les élèves que ce que l’auteur suggère.   L’idée est de séparer la page en quatre quadrants et de débuter les notes à partir du coin supérieur gauche avec le type 1.  

1. Haut gauche (Type 1):  je guide les élèves avec des exemples comme [x] = 5 et [x] = — 9
2. Haut droite (Type 2):  les élèves résolvent seuls, par exemple[2x] = 9 et [\( \frac{x}{2} \)] = 5
3. Bas droite (Type 3):  ils choisissent et résolvent un exemple comme [— x] = 8 ou — [\( \frac{x}{2} \)] = — 5
4. Bas gauche: les élèves notent les points clés à retenir dans deux semaines.

Ce format structuré aide à organiser leurs apprentissages de manière durable. Voici un exemple de ce à quoi cela pourrait ressembler :

Cette expérience m’a convaincu de l’efficacité du « thin slicing ». Une fois maîtrisée, cette approche facilite la création d’activités similaires. Je vous invite à découvrir d’autres de mes activités sur la fonction partie entière et la factorisation algébrique pour la 4e secondaire sur le site du GRMS. Je continue néanmoins à proposer occasionnellement des problèmes en suivant le référentiel d’intervention en mathématique. Pour ceux qui souhaitent explorer ou approfondir leurs connaissances sur cette pratique pédagogique, je vous recommande le congrès du GRMS qui aura lieu à Sherbrooke, du 5 au 7 novembre 2025, et où Peter Liljedahl sera présent. Rien ne vaut une expérience directe pour mesurer l’impact de cette approche sur l’engagement et l’apprentissage des élèves.