Leçons de la classe de mathématiques
Leçons de la classe de mathématiques
La simplification d’expressions
- 9 minutes de lecture
Jérôme Proulx
- Laboratoire Épistémologie et Activité Mathématique
- Université du Québec à Montréal
- proulx.jerome@uqam.ca
En tant que didacticien des mathématiques, je suis amené par mes travaux de recherche à être en classe et à travailler avec des élèves tant du primaire, du secondaire que de l’université. Lors de ces visites et de ces travaux, les élèves m’offrent souvent ce que j’appelle des perles mathématiques, à travers divers raisonnements, erreurs, questions, stratégies et solutions. C’est à partir de ces productions mathématiques que je propose de tirer des réflexions, voire quelques leçons, tant mathématiques que didactiques, dans le but de comprendre ce que les élèves nous enseignent parfois par leurs activités mathématiques…
L’après-midi bat son plein et les élèves travaillent fort à résoudre les tâches que je leur propose sur le pourcentage en contexte de calcul mental. Avec l’approbation de leur enseignant, je décide de leur proposer une dernière tâche, une « belle », un défi. La tâche est de me dire combien vaut l’expression suivante:
\( \frac{25\%}{75\%} \)
Ils ont 15 secondes pour y penser et ensuite, en levant la main, m’expliquer leur réponse chacun à leur tour. J’aperçois rapidement, dès la pose de la tâche au tableau, que certains écarquillent les yeux, alors que d’autres froncent les sourcils. Bien que j’aie repêché cette tâche dans un manuel scolaire, elle ne leur semble pas habituelle. Je suis curieux de voir comment ils vont s’engager dans celle-ci.
Un premier élève tente sa chance. Il propose de transformer les pourcentages en nombres décimaux. Ainsi, 25% devient 0,25 et 75% devient 0,75, mais il hésite pour l’ordre de la division de ces nombres décimaux, donc entre les réponses 3 et 0,333 … C’est une difficulté courante et même bien documentée par les travaux relatifs aux opérations avec les nombres décimaux. Un autre élève, Marco, intervient alors pour offrir sa stratégie et faire avancer cette réflexion.
Marco propose d’ajouter 25% aux deux pourcentages de l’expression \( \frac{25\%}{75\%} \). Ainsi, comme 75% + 25% donne 100%, il explique devoir faire la même chose « en haut ». Avec 25% + 25% qui donne 50%, il aboutit à l’expression \( \frac{50\%}{100\%} \). Les traces suivantes sont inscrites au tableau:
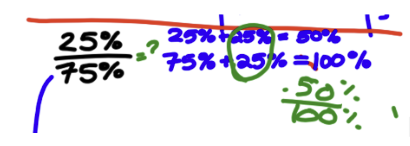
Je demande à Marco pourquoi il ajoute 25%. Il me répond que « C’est plus simple à calculer quand les nombres sont ronds ». C’est bien vrai, me dis-je, tout en n’étant pas certain de bien comprendre où il voulait en venir avec cela. Et, alors que je continue de noter au tableau les explications de Marco, je ne peux m’empêcher d’entendre les différentes réactions d’inconfort de la part des autres élèves, avec des « Mais ça devient pas équitable ! » ou encore « Mais ça fait pas des fractions équivalentes ! ». Marco se lève et vient au tableau en continuant à expliquer que \( \frac{50\%}{100\%} \) est beaucoup plus simple que \( \frac{25\%}{75\%} \), disant « Là, je l’ai simplifiée ! ». Vrai encore, il n’a pas tort, je me dis, mais je demeure tout de même perplexe, et les autres élèves aussi ! Il ajoute: « Si je veux faire un calcul, ça va être plus facile à calculer si tes nombres sont ronds au lieu d’avec 25 et 75. ». Le questionnement continue, et d’autres réponses sont proposées comme \( \frac{1}{3} \), \( 0,\overline{3} \) et \( 33,\overline{3} \% \). Toutefois, plusieurs élèves veulent relancer Marco pour en savoir davantage sur ses ajouts de 25%. La discussion suivante a alors lieu au sujet de \( \frac{25\%}{75\%} \) et \( \frac{50\%}{100\%} \):
| Marin : | Ses [deux] réponses sont différentes. |
| Domi : | Moi j’aimerais bien comprendre où il a pris ses deux 25. |
| Jérôme : | Pour rendre ça plus facile, il nous a dit. |
| Marin : | Mais il aurait pu prendre n’importe quel chiffre ! |
| Jérôme : | [à Marco] Pourquoi 25 et pourquoi pas 12 ou pourquoi pas 8 ? |
| Marco : | Parce que j’ai vu que 25 et 25 donne 50 et que si j’ajoute aussi 25 ça donne 100. |
| Jérôme : | Des nombres ronds … |
| Marco : | Exact. |
La période achève, et le questionnement demeure vif. Les élèves portent attention aux autres réponses offertes précédemment, mais l’ajout des 25% continue d’intriguer. La cloche sonne…
Que tirer de tout ceci ?
Une première réaction face à cette idée d’ajout de 25% est de se dire que Marco ne comprend pas beaucoup la tâche donnée et qu’il fait un peu n’importe quoi. C’est en effet ce que certains élèves semblent vouloir exprimer lorsque Marco explique sa stratégie. En même temps, la tâche proposée est inhabituelle et est difficile (elle leur a même été annoncée ainsi). C’est peut-être un peu normal de recevoir des réponses « surprenantes » de la sorte. Mais que tente de faire Marco?
En reliant le « +25% » avec le fait que la tâche est inhabituelle et comporte son lot de défis, une façon de comprendre l’idée de Marco est qu’il tente de rendre la tâche plus accessible, plus facile à résoudre. C’est ici que son idée de « simplifier » entre en ligne de compte. En voulant simplifier l’expression, l’idée d’ajouter 25% semble raisonnable, car \( \frac{50\%}{100\%} \) est plus facile à évaluer que \( \frac{25\%}{75\%} \). Et, c’est probablement ce que Marco affirme lorsqu’il dit: « Là, je l’ai simplifiée !».
Le problème que nous voyons avec la stratégie de Marco est que l’ajout de 25% à chacun des pourcentages a transformé l’expression \( \frac{25\%}{75\%} \) au point d’en perdre l’équivalence avec la nouvelle expression obtenue: \( \frac{25\%}{75\%} \) ≠ \( \frac{50\%}{100\%} \). C’est ce que certains élèves soulignent. En effet, bien que \( \frac{50\%}{100\%} \) soit peut-être plus facilement manipulable ou calculable, sa valeur n’est malheureusement pas équivalente à celle de l’expression initiale. La stratégie de Marco ne réussit pas. Elle réussit par contre sur autre chose.
Une chose importante qui ressort des explications de Marco est justement quelque chose qu’il n’a pas dit : jamais Marco n’a affirmé explicitement que \( \frac{25\%}{75\%} \) et \( \frac{50\%}{100\%} \) représentent des expressions équivalentes. Sur la base de ce qu’il répond aux autres élèves, et à mes questions, il n’est pas clair qu’il considère ces deux expressions comme étant équivalentes. En fait, son objectif semble tout autre, soit de chercher une façon de simplifier la tâche. Et sur ce point, il est impossible de le prendre en défaut : Marco a bel et bien rendu la tâche plus simple ! De notre côté, nous y voyons peut-être un problème, car l’équivalence entre les deux expressions n’est pas conservée, mais ce n’est pas ce que Marco semble vouloir faire avec son ajout de 25%. En ce sens, il n’a pas tort de dire que les calculs en sont simplifiés, bien qu’il en ait toutefois perdu l’équivalence. C’est une bonne idée, mais elle ne nous aide peut-être pas beaucoup à trouver la valeur de l’expression.
Mais il y a plus !
Même si la stratégie de Marco ne nous aide pas à trouver la valeur de \( \frac{25\%}{75\%} \), elle met en évidence un deuxième élément important qui mérite notre attention. Ce qui frappe est que Marco réutilise presque mot pour mot ce qui est habituellement prononcé pour justifier l’importance de devoir simplifier des expressions (par exemple des fractions, des expressions algébriques) : si tu veux faire des calculs, il est important de (savoir) simplifier pour faciliter ton travail ! Il est en effet plus complexe de travailler avec \( \frac{27}{63} \) que \( \frac{3}{7} \), et transformer l’équation \( 3x^2 + 7xy \; – \; 6x^2 + 3xy +‒6 = 9 \) en une version plus compacte peut grandement nous simplifier la vie.1
Le fait que Marco réutilise presque textuellement les justifications habituelles pour expliquer l’importance de la simplification d’expressions est très parlant, car cela met en évidence certains éléments que nous gardons possiblement cachés, sûrement sans nous en rendre compte. Et c’est ici que Marco, un peu sans le savoir, nous fait la leçon : il nous rappelle que l’idée de conserver l’équivalence des expressions est un des aspects les plus fondamentaux de la simplification d’expressions. Cette idée est devenue tellement évidente pour nous que nous la tenons probablement pour acquise et la laissons implicite dans notre discours. Pourtant, l’équivalence est au cœur pour nous tous du concept même de simplification d’expressions.
Et c’est un peu ce que Marco nous souligne. Sa stratégie pointe sur la pertinence de mettre au premier plan cette idée d’équivalence lors du travail de simplification d’expressions, et ce, pour éviter que « simplification » et « équivalence » en deviennent des concepts dissociés. Par sa stratégie surprenante d’ajout de 25%, Marco nous rappelle que de rendre plus simple une expression n’est pas en soi suffisant pour en évaluer la valeur, et qu’il est primordial de s’assurer de rendre explicite l’équivalence de ces mêmes expressions lors de leur simplification.
Et ça, c’est toute une leçon ! Merci Marco !
Références
Proulx, J. (2021). Toutes ces réponses sont bonnes. Multimondes.
Articles dans ce numéro

Mot de la Directrice
Il me fait plaisir de vous présenter votre tout nouveau numéro de la revue Envol,

Le GRMS : Alimenter la réflexion
Je suis heureux de vous présenter ce nouveau numéro de notre revue, un moment privilégié

Hommage à Pierre Couillard, plus qu’un « brancheux » de fils
Son entrée dans le monde de l’éducation, à la fin des années 1980, où les

La classe collabo-réflexive en mathématiques : un bref survol
Une classe collabo-réflexive se distingue par son dynamisme : les élèves, debout et répartis dans

La partie entière, tranchée mince : une approche BTC en action
Ce chapitre explique comment maintenir l’intérêt des élèves grâce au « thin slicing », illustré

Desmos Mode Examen : un outil équitable pour soutenir l’évaluation en mathématique et favoriser la réussite
Parmi les outils numériques disponibles, la calculatrice graphique de Desmos s’est rapidement imposée comme une

Évaluer autrement: tâche flexible, créative et colorée en mathématiques CST et TS de cinquième secondaire
Probablement comme plusieurs d’entre vous, nous trouvons important de présenter à nos élèves des tâches

Parole aux communautés de pratique interordres secondaire-collégial en mathématiques
Comment faciliter la transition secondaire-collégial en mathématiques des élèves finissants de 5e secondaire qui feront

Leçons de la classe de mathématiques
L’après-midi bat son plein et les élèves travaillent fort à résoudre les tâches que je
Un codage à la Gödel
Le but de ce court texte est de partager une idée avec laquelle j’avais jonglé

La manipulation au secondaire : est-ce vraiment nécessaire ?
Lors du dernier congrès du GRMS, Geneviève Dupuis, conseillère pédagogique du Récit de l’enseignement privé,

5e article: la marche aléatoire (probabilltés)
Récit #5 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Marche aléatoire

Défis Opti-Math
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à

Défis Opti-Math – Solutions
Solutions des questions du Défi Opti-Math. Un défi mathématique pour tous les élèves du secondaire.

