Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Un codage à la Gödel

(27 • 315 • 54 • 75  • 1112 )

  • 9 minutes de lecture
Picture of Vincent L. Rouleau

Vincent L. Rouleau

Une intention particulière sur le plan de l'enseignement des idées mathématiques

Le but de ce court texte est de partager une idée avec laquelle j’avais jonglé lors du printemps 2022, puis mise à l’essai au cours de l’année scolaire qui a suivi.

L’intention première était née de mon insatisfaction quant aux activités ou exercices que j’avais rencontrés qui permettaient à des élèves de 14-15 ans (3e secondaire) de jouer avec la notation exponentielle; il m’avait souvent semblé que les contextes manquaient d’authenticité. L’idée simple, mais pas simplette, que j’ai voulu explorer, consistait à mettre en place un contexte ludique de décryptage de messages présentés sous la forme de nombres. Voici comment :

  1. Pour coder un mot, on associe d’abord la position de chacune de ses lettres (de gauche à droite) à une base première, de telle sorte que la base de la ne lettre correspond au ne nombre premier. Par exemple, dans le mot « aha », le premier « a » correspond à la base 2, le « h » à la base 3 et le deuxième « a » à la base 5.
  2. Ensuite, chaque lettre de l’alphabet latin est associée à un nombre naturel de telle sorte que l’ordre usuel est préservé, c’est-à-dire « a » correspond à 1, « b » à 2, « c » à 3, etc. Ce nombre sera l’exposant affecté à la base qui indique la position de la lettre.
  3. Enfin, on code le mot en affectant à chaque base (la position de la lettre) l’exposant (correspondant à la lettre) et en considérant le nombre formé par leur multiplication. Ainsi, le mot « aha » codé sera 21 • 38 • 51, c’est-à-dire 65 610.

Comme un mot codé prend souvent la forme d’un très grand nombre, le recours à une notation exponentielle se justifie naturellement1. Aussi, une première contribution de ce jeu de décodage qui m’était venue à l’esprit était de servir de contexte pour amener les élèves à découvrir les petits théorèmes des exposants naturels2 et à les appliquer. Voici un exemple de séquence de mots à décoder conçue dans ce sens:

  1.   23 • 32 • 25 • 33 • 4
  2.   711 • 34 • 27 • 112 • 56 • 6 • 25 • 73 • 58 • 8 • 75 • 113
  3.   7 • (32)3 • ((52)3)2 • (22)2 • 52 • 49 • (33)3
  4.   2 • (2 • 3)3 • (23 • 3)2
  5.   (32 • 53) • (32 • 143)4 • 427

En plus de réactiver l’associativité et la commutativité de la multiplication, il me semble invitant d’avoir recours naturellement à quelques raccourcis, tels que bm • bn = bm+n (à partir de (i) et (ii)), (bm)n (à partir de (iii)) et (a • b)m = am • bm (à partir de (iv)).

Ce terrain de jeu peut être mis à contribution pour l’enseignement et l’apprentissage dans différentes directions. En voici quelques-unes que j’ai explorées:

  • À partir du moment où le jeu a été compris par les élèves, il est possible de le réinvestir tout au long de l’année scolaire afin de réactiver les habiletés de manipulation avec la notation exponentielle. Par exemple, voici un message festif en quatre mots partagé en décembre:
    1. 54 • 182 • 57 • 153 • 38
    2. (24 • 3)5 • ((52 • 113)3 • 78)2 • 55
    3. \( \sqrt[3]{2^8 \cdot 3^{10}} \) • \( \sqrt[3]{5^{25}} \) • \( \sqrt[3]{5}^{32} \)
    4. \( \frac{2^{13} \cdot 3^{-6} \cdot (7 \cdot 11^{-3})^{-4}}{(2^{-1} \cdot 5 \cdot 11)^{-7} \cdot 5^{-13} \cdot 3^{-11} \cdot 7^{-9}} \)

Et en voici un donné en juin3:

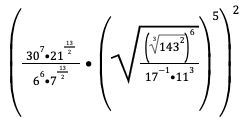
  • Le jeu de décodage offre une possibilité de rétroaction à des fins de validation. En effet, des erreurs commises en cours de route peuvent être révélées par l’obtention d’un mot mal orthographié, identifiées en retraçant les manipulations effectuées sur la base première et les exposants correspondant à une lettre donnée, puis corrigées. Ainsi n’est-il pas surprenant que presque la totalité des élèves aient réussi à décoder correctement le mot suivant lors d’une situation d’évaluation:

5 • 75 • 142 • 1112 • 2115 • 333

  • Notons que, lorsque le nombre à décoder est exprimé avec des facteurs qui sont des nombres composés, l’élève est forcément amené à le factoriser en nombres premiers. Cette habitude peut devenir une stratégie et être réinvestie dans d’autres contextes; observons par exemple la résolution de l’équation ci-dessous par une élève à la toute fin de l’année scolaire:

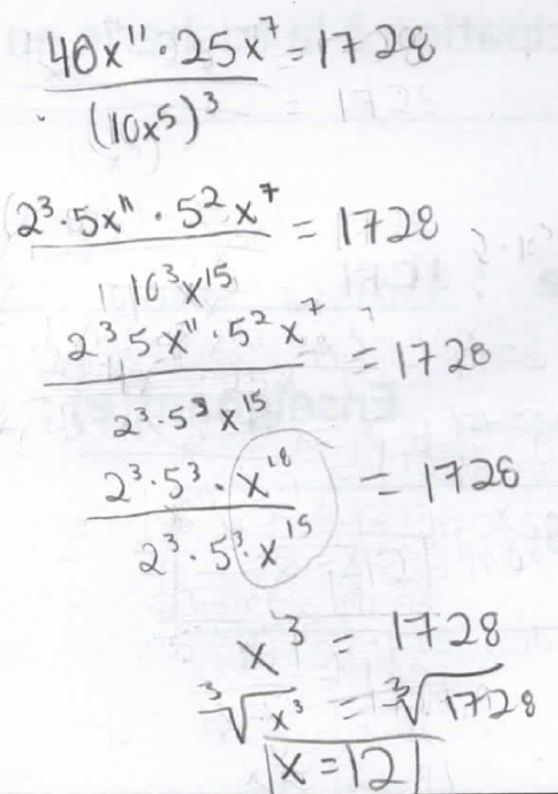
  • Comme dans plusieurs situations rencontrées en mathématique, il est possible, voire souhaitable, de jouer dans un sens (décodage) et dans l’autre (codage). Une activité qui consiste à coder son propre message pourrait être appréciée par certains élèves et encourager leur esprit créatif. Ce fut vraisemblablement le cas lors d’un exercice facultatif à faire à la maison qui consistait à coder son prénom tout en respectant minimalement certaines contraintes, par exemple l’usage de la notation avec un radical. D’ailleurs, l’élève dont le prénom est codé ci-dessous semble même avoir pris un malin plaisir à donner du fil à retordre à son enseignant qui a dû le décoder !

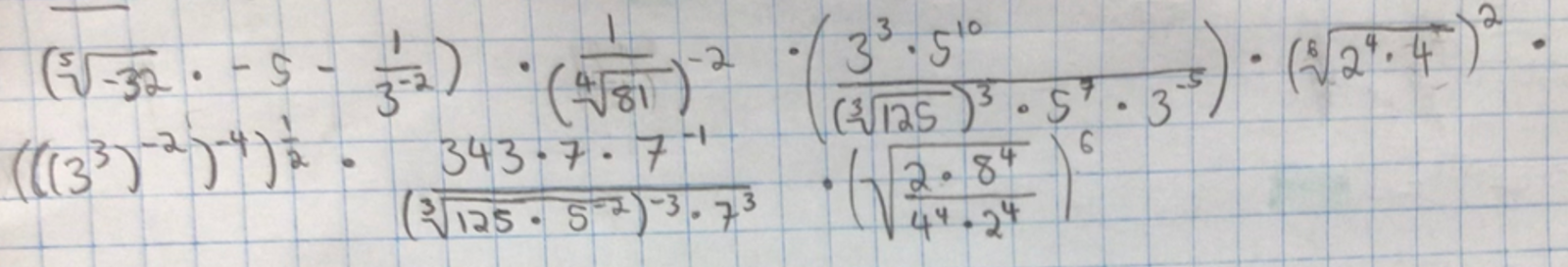
En bref, ce jeu de décodage ou de codage me semble bien répondre à différentes attentes d’un milieu didactique visant à enseigner une idée mathématique. Le fait que l’on doive obtenir un mot ou un énoncé « bien formulé » à la suite du décodage rend la tâche signifiante pour les élèves, facilitant la dévolution et l’autorégulation. Cela dit, il possède également une valeur éducative encore plus importante à mes yeux dont j’aimerais brièvement discuter dans la prochaine section.

Une intention générale sur le plan de l’éducation mathématique

À première vue, le jeu que j’ai présenté pourrait n’être finalement qu’un jeu de plus parmi les autres, conçus pour chercher à rendre l’apprentissage moins aride pour les élèves, peut-être même en amuser certains au passage, mais qui n’a pas d’autre finalité. Un tel jeu risquerait d’être mathématiquement pauvre et cela me semblerait très insatisfaisant.

Or, voici l’aspect qui, je pense, le distingue de certains autres: il facilite un rapprochement avec quelques éléments de culture mathématique pouvant être partagés aux élèves.

D’une part, on pourrait amener ces derniers à se demander : se pourrait-il que deux différents mots correspondent à un même nombre ? Ce questionnement est riche mathématiquement et permet de discuter du théorème fondamental de l’arithmétique qui énonce que tout nombre composé peut s’exprimer d’une unique façon comme multiplication de nombres premiers (si l’on ne tient pas compte de l’ordre des facteurs). D’ailleurs, ne devrions-nous pas le plus souvent possible – au moins à chaque année de scolarité des élèves – chercher une occasion de réinvestir la notion de nombres premiers ? Dans un autre ordre d’idées, on pourrait en arriver à se questionner sur la possibilité de coder autrement les mots en nombres et discuter des avantages ou désavantages; on peut penser par exemple aux moyens utilisés pour le codage et le décodage d’un texte en « nombres binaires » afin de le transférer d’un ordinateur à un autre.

D’autre part, remarquons qu’il ne serait pas sécuritaire de nos jours d’envoyer des messages secrets codés de la façon proposée dans notre jeu; un message intercepté pourrait être décrypté à la main par un élève de 14 ou 15 ans, et à plus forte raison, à l’aide d’un ordinateur. Mais à quoi donc ce codage pourrait-il vraiment servir ? Je révèle enfin la genèse de mon idée: il s’agit en fait d’un codage inspiré de celui utilisé par Kurt Gödel pour démontrer son célèbre théorème d’incomplétude, dont l’importance pour les fondements de la mathématique est probablement au moins aussi grande que celle de la théorie de la relativité d’Einstein pour la physique. Et l’utilité du codage n’était ni plus ni moins que de faire correspondre tout énoncé (formulé dans un langage) à un nombre, et ce, de façon biunivoque, de sorte que l’on pouvait par la suite raisonner avec des nombres en lieu et place des énoncés !

En pensant au lecteur que j’ai peut-être indirectement invité à en apprendre davantage sur Gödel et son théorème, je soulève le questionnement suivant: y a-t-il « asymétrie »  entre notre culture scientifique (autre que mathématique) et notre culture proprement mathématique ?  Même sur le plan d’une culture en surface, à la vue de l’un ou l’autre des fameux clichés de Kurt Gödel et d’Albert Einstein côte à côte à l’Institute for Advanced Study de Princeton, entend-on plus souvent demander « Qui est à côté d’Einstein ? » ou « Qui est à côté de Gödel ? »

J’essaie toujours de garder à l’esprit que l’enseignement des mathématiques s’inscrit plus largement dans le cadre de l’éducation mathématique. Et à titre d’enseignant, je crois qu’il est de mon devoir de saisir ou de provoquer les occasions de partager une certaine culture mathématique. Non seulement en surface, par exemple en présentant aux élèves les noms de mathématiciens ou les énoncés de théorèmes, mais également plus profondément en les invitant à faire les premiers pas menant aux grandes idées et en les amenant à découvrir les liens parfois surprenants qui les unissent.

Merci à mon collègue Simon Gauthier pour ses commentaires avisés à la suite de la lecture d’une première version de ce texte.

  1. J’avais au départ pensé faire l’usage de la notation dite scientifique pour exprimer un mot codé, mais elle s’avère tout aussi fastidieuse à exprimer et à décoder que le nombre écrit en notation décimale; en voici un exemple:

    2. 6,69462604992 x 10 31

    Et puis, j’avais l’impression de dénaturer la raison d’être de cette notation qui devrait rester fidèle aux contextes où l’on cherche essentiellement à exprimer l’ordre de grandeur d’une valeur (souvent approximée).

  2. Que l’on nomme communément « lois des exposants » dans la culture scolaire, mais je préfère éviter cette appellation qui pourrait tout aussi bien évoquer un décret arbitraire tombé du ciel. Dans cette situation, parler plutôt de « théorèmes » invite mathématiquement à la possibilité de les découvrir – sous la forme de conjectures – et à en esquisser une preuve.
  3. À la suite de la suggestion d’une élève, un facteur premier absent (ou avec un exposant nul) indique un espace entre deux mots.

Références

  • Fortier, J. (2016). Une preuve moderne du théorème d’incomplétude de Gödel. Bulletin de l’AMQ, 56 (3), 27-44.
  • Grannec, Y. (2012). La Déesse des petites victoires. Paris : Éditions Anne Carrière.
Partagez

Articles dans ce numéro

Se connecter