La transition secondaire-collégial
en mathématique
- 6 minutes de lecture
Auteurs:

Nathalie Cormier,conseillère pédagogique, CSS Des Sommets (CSSDS)

Caroline Fortier, enseignante, CSS des Hauts-Cantons (CSSHC)

Chantal Gauvreau, enseignante, Cégep de Sherbrooke
Chaque année, des milliers d’élèves québécois franchissent une étape charnière dans leur parcours scolaire : le passage du secondaire au cégep. Ce moment de transition, bien que porteur de nouvelles possibilités, s’accompagne aussi de défis importants, notamment en mathématique, où les attentes et les approches pédagogiques peuvent varier considérablement d’un ordre d’enseignement à l’autre.
Dans ce contexte, il devient essentiel de créer des ponts entre les personnes enseignantes du secondaire et celles du collégial afin de mieux comprendre les réalités respectives, d’harmoniser les pratiques et de soutenir les élèves dans leur cheminement. C’est dans cette optique qu’une collaboration régionale a été mise en place en Estrie, réunissant personnes conseillères pédagogiques (CP) et personnes enseignantes des deux ordres autour d’un objectif commun : faciliter la transition scolaire en mathématique.
Cet article présentera les apprentissages issus de cette démarche collaborative, quelques constats partagés sur les différences entre les ordres d’enseignement, ainsi que des réflexions soulevées quant aux leviers à activer pour mieux les préparer à la réalité collégiale. C’est donc en janvier 2020 que s’est amorcée une discussion entre CP du secondaire et du cégep ainsi que d’une enseignante du collégial libérée d’une partie de sa tâche pour ce projet, madame Julie Tremblay. À la suite de nombreuses discussions et après avoir sondé des personnes enseignantes, nous avons précisé notre objectif de travail afin d’analyser les fragilités liées au cours de Calcul différentiel. Après avoir travaillé sur une progression des apprentissages (PDA) entre le secondaire et le collégial, une personne enseignante de chaque centre de services (CSS) et des personnes enseignantes du cégep se sont jointes à l’équipe de travail. L’objectif n’était pas que les personnes enseignantes du collégial dirigent vers des façons de faire celles du secondaire, mais bien de comprendre la réalité de chaque ordre, selon leurs encadrements respectifs. Au terme de tous ces échanges enrichissants, une grande rencontre régionale a été organisée afin de partager quelques-uns des constats à la suite d’un sondage à l’attention des personnes enseignantes des deux ordres. Par exemple, nous avons constaté que plusieurs personnes enseignantes connaissent moyennement le contenu des cours de mathématiques dans l’autre ordre d’enseignement, et ce, particulièrement sur la manière ou la façon dont les contenus sont abordés et sur le contexte dans lequel ils sont présentés (exigence auprès des élèves, complexité des problèmes, etc.).
Voici un extrait du tableau comparatif entre le Cégep de Sherbrooke et les trois CSS participants :
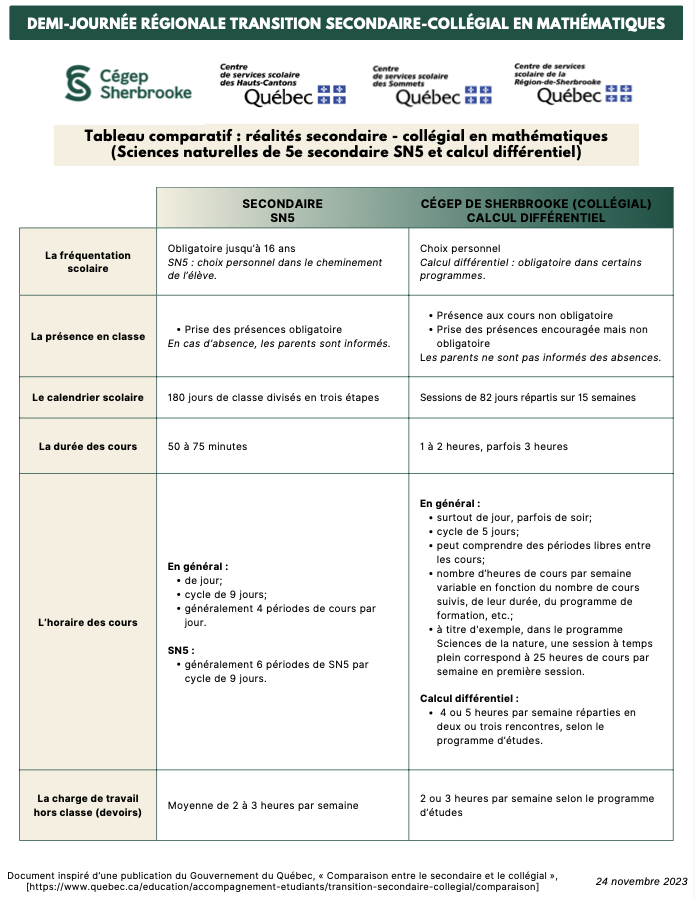
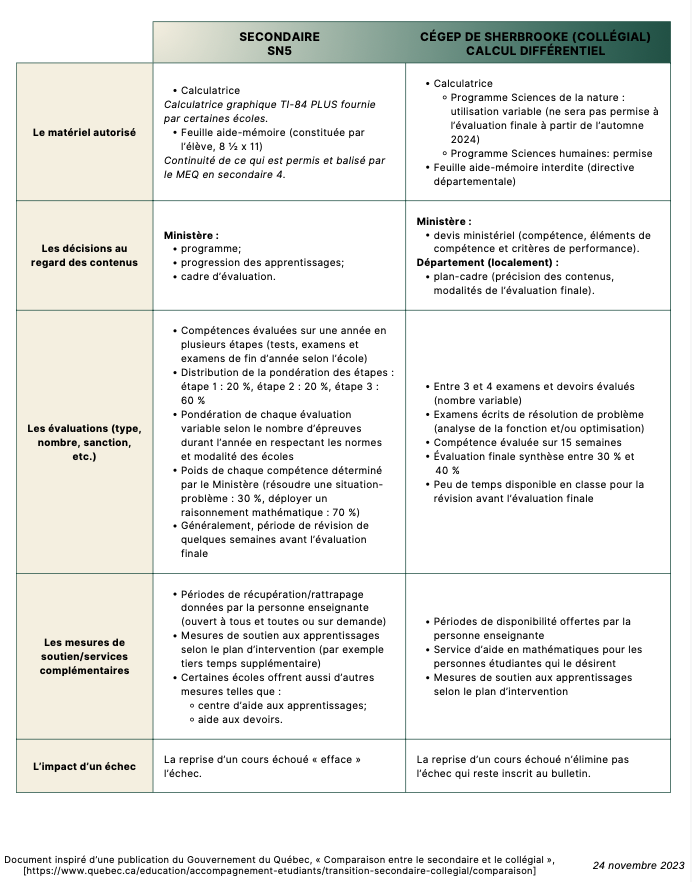
Lors de nos discussions, le collégial a constaté qu’il y avait une certaine rigidité dans le programme du secondaire, cela étant dû au fait que les programmes et la PDA qui en découle sont fixés par le MEQ. Par exemple, certaines notions, principalement vues en 3e et en 4e secondaires, étaient très utilisées au Cégep et ne faisaient pas partie spécifiquement du programme de 5e secondaire. En créant la PDA vers le collégial, cela a permis de sélectionner des connaissances du secondaire qui sont réutilisées dans le cours Calcul différentiel et d’ajouter des précisions quant à certains thèmes qui sont spécifiques au collégial.
Extrait de la PDA modifiée


Enfin, des discussions sur des notions plus spécifiques, comme les fonctions, les graphiques et les manipulations algébriques, nous ont permis d’adapter certaines pratiques. Certaines personnes enseignantes ont décidé de revoir les notations utilisées, d’ajuster leur utilisation de vocabulaire spécifique (entre autres quant aux asymptotes) ou d’accorder davantage d’importance aux connaissances préalables. De manière générale, toutes et tous s’entendaient pour dire que les manipulations algébriques et l’utilisation des lois des exposants étaient une fragilité commune aux deux ordres. Afin de diminuer celles-ci, mesdames Caroline Fortier et Catherine Huppé, enseignantes au secondaire, ont même créé des défis mathématiques liés aux fragilités afin de favoriser le passage vers le cégep.
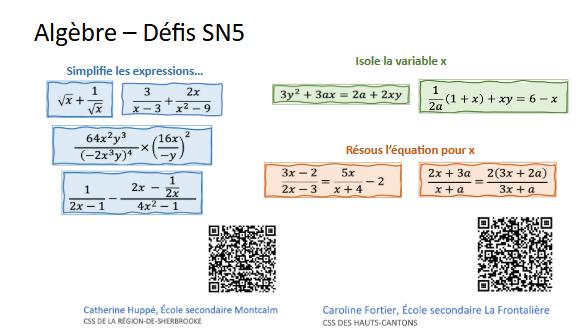
En conclusion, le travail de collaboration n’est pas terminé, car d’autres initiatives sont dans la mire pour la poursuite des chantiers. Les résultats des élèves se sont-ils améliorés ? Cela est difficile à dire… Cependant, des pratiques ont évolué et toutes et tous souhaitent une meilleure réussite des élèves. En vue de l’année 2025-2026, d’autres personnes enseignantes se sont jointes à l’équipe, ce qui a soulevé d’autres préoccupations, lesquelles suggèrent des pistes de travail intéressantes. Les étudiants ont-ils le même profil qu’avant ? Comment travaillent-ils et apprennent-ils au-delà des maths ? Des discussions fort enrichissantes sont à poursuivre…
Références
BOLDUC, A. (2020). Analyse d’interventions menées par une orthopédagogue du secondaire qui contribuent à l’expression d’un contrôle en mathématiques chez des élèves en difficulté d’apprentissage. [Mémoire de maîtrise, Université du Québec à Montréal].
CENTRE DE TRANSFERT POUR LA RÉUSSITE ÉDUCATIVE DU QUÉBEC. (2018). Deuxième dossier : L’utilisation des données au service de l’apprentissage, Québec, QC : Auteur. Repéré à [https://rire.ctreq.qc.ca/wp-content/uploads/2018/09/CTREQ-Projet-Savoir-Utilisation-des-données-C2-30117-Cliquable.pdf].
DUFOUR, R., DuFour, R., Eaker, R., W. Many, T. et Mattos, M. (2019). Apprendre par l’action : Manuel d’implantation des communautés d’apprentissage professionnelles (3e éd.), Presses de l’Université du Québec.
MESSIER, G. (2020) Comment réfléchir ou enrichir sa planification à l’aide de la démarche didactique, Dans N. Granger, L. Portelance et G. Messier (dir.) Planifier son enseignement au secondaire (33-46), JFD éditions.
MINISTÈRE DE L’ÉDUCATION ET DE L’ENSEIGNEMENT SUPÉRIEUR (2020). Guide pour la mise en place de la réponse à l’intervention, Québec, [https://drive.google.com/file/d/1cotUOFEvWzG3h5vm9X7Z66Ry8PX2M99r/view].
MINISTÈRE DE L’ÉDUCATION ET DE L’ENSEIGNEMENT SUPÉRIEUR (2016). Progression des apprentissages au secondaire : Mathématique, Québec, [https://www.education.gouv.qc.ca/fileadmin/site_web/documents/education/jeunes/pfeq/PDA_PFEQ_mathematique-secondaire_2016.pdf].
Articles dans ce numéro

Mot de la Directrice
Il me fait plaisir de vous présenter votre tout nouveau numéro de la revue Envol,

Alimenter la réflexion : le thème inspirant du Congrès 2025 !
C’est avec une immense joie et une grande effervescence que nous nous préparons à vous

Compétences en construction : décomposer pour mieux apprendre
Développer les compétences mathématiques grâce à la tâche découpée, une approche structurée qui soutient la

Le Grand Programmathon
Le Grand Programmathon est une compétition de conception de jeux vidéo. Elle se déroule sous

Les tours de Hanoï – L’apprentissage par le jeu
L’apprentissage par le jeu est une stratégie pédagogique intéressante due au plaisir qu’elle procure aux

Pour une approche plus simple de l’enseignement des logarithmes
Au moins une fois par décennie, mon meilleur ami m’appelle au téléphone pour me parler

Arrimer l’enseignement en classe et l’orthopédagogie en mathématiques au secondaire
Lors de l’élaboration de son projet éducatif en 2023-2024, l’école secondaire de l’Odyssée a identifié,

La transition secondaire-collégial en mathématique
Chaque année, des milliers d’élèves québécois franchissent une étape charnière dans leur parcours scolaire :

Les mathématiques du sofa
Un sofa doit être déplacé le long d’un corridor en L. Si on souhaite que

L’importance des tâches hors curriculum dans la mise en place de la classe collabo-réflexive
Des élèves qui réfléchissent sont des élèves engagés, actifs et construisant leurs propres savoirs ainsi

Est-ce que 4 + 22 % = 22 % + 4 ? (Ou la richesse mathématique du concept de %)
Le titre de l’article soulève une drôle de question. C’est intentionnel, tout autant que c’est

Célébrer la Journée internationale des mathématiques le 14 mars 2026
En 2026, le 14 mars est un samedi… Mais, les occasions de célébrer avec les

Défis Opti-Math
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à

Défis Opti-Math – Solutions
Solutions des questions du Défi Opti-Math. Un défi mathématique pour tous les élèves du secondaire.

