Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Les tours de Hanoï

L’apprentissage par le jeu

  • 5 minutes de lecture
Picture of Vincent Roy

Vincent Roy

L’apprentissage par le jeu est une stratégie pédagogique intéressante due au plaisir qu’elle procure aux apprenants. Ces derniers entrent dans un univers où l’apprentissage s’effectue presque sans qu’ils ne s’en rendent compte. 

Dans ma classe, je fais beaucoup d’activités liées aux jeux. Qu’ils soient mathématiques ou non, ces jeux nous aident à passer du temps en changeant les routines. L’un de mes préférés est celui des tours de Hanoï. Ce jeu m’a toujours impressionné. J’en ai un dans ma classe et souvent les élèves se mettent à jouer et tentent de le résoudre avec le plus d’étages possible. Lorsque mes élèves s’amusent en résolvant un casse-tête mathématique et tentent de découvrir une logique, je suis aux anges. 

Le jeu des tours de Hanoï, inventé par le mathématicien français Édouard Lucas en 1883, est un défi classique qui combine logique et réflexion. Son principe est simple : déplacer un ensemble de disques de tailles différentes d’une tige à une autre, trois tiges au total, en respectant la règle qu’une grande rondelle ne peut être par-dessus une petite rondelle. Le but est aussi de minimiser le nombre de déplacements pour y arriver. 

Ce jeu cache une structure mathématique fascinante. En effet, le nombre minimal de mouvements nécessaires pour résoudre ce casse-tête suit une progression exponentielle lorsque le nombre de disques augmente, offrant ainsi une occasion d’illustrer l’application des fonctions exponentielles dans un contexte concret. 

Vous connaissez sûrement la collection des revues Accromath, collection que je possède dans ma classe et que je fais parfois lire à mes élèves. L’idée de faire un projet sur les tours de Hanoï m’est venue d’un article de cette revue.

 https://accromath.uqam.ca/2016/02/les-tours-de-hanoi-et-la-base-trois/ 

Cet article explore le lien entre les tours de Hanoï et les mathématiques, en montrant comment ce jeu peut être un outil pédagogique pour comprendre les principes des fonctions exponentielles. Je cherchais un moyen de l’intégrer dans un cadre éducatif autrement que par la simple lecture de l’article.

Lorsque j’enseigne, j’insiste souvent sur l’exactitude des résultats que l’on obtient, sur le degré de précision d’une réponse. Je m’amuse à donner des exemples de la vie, comme l’ébéniste qui travaille avec le bois souvent dispendieux. Ce dernier travaille avec une précision allant jusqu’au \( \frac{1}{64}^{\text{e}} \). Et là, BINGO ! Je réalise que j’ai une idée. Pourquoi ne pas aller en atelier de technologie pour faire construire aux élèves leur propre tour de Hanoï ? Les élèves adorent, en général, aller en atelier de menuiserie.

À la suite de la confection de leur jeu, je donne du temps en classe afin de permettre aux élèves de s’amuser un peu avec leur tour et ainsi, cumuler des données pour les présenter ensuite sous forme de table de valeurs liant le nombre de rondelles dans le jeu et le nombre minimal de coups pour déplacer la tour.

La table de valeurs qui représente le nombre de déplacements en fonction du nombre de rondelles est intéressante pour amener les élèves à faire la découverte de la règle sous la forme f(x) = a(c)x + k.

Les élèves peuvent d’abord observer que l’accroissement du nombre de déplacements au niveau 1 augmente de façon logique, mais ils peuvent surtout constater qu’au deuxième niveau, il existe un lien multiplicatif constant, ce qui distingue la fonction exponentielle des fonctions polynomiales précédemment étudiées. Ces accroissements permettent aux élèves de prédire plus de données.


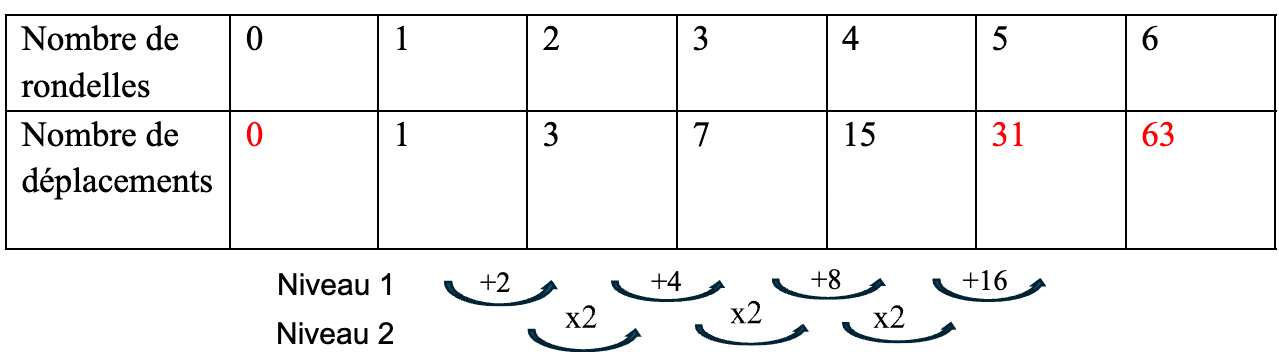
Dans la table de valeurs, les données en rouge sont les prédictions que les élèves peuvent faire après avoir observé la progression. D’ailleurs, en « reculant » dans la table de valeurs, ils peuvent déterminer la valeur initiale, qui correspond à a + k.  Oh que c’est beau ! 

On voit apparaître le système d’équations ci-dessous lorsque l’on substitue les coordonnées (0, 0) et (1, 1) dans l’équation D(n) = a • 2n + k.

① a + k = 0

② 2a + k = 1

De là, les élèves déduiront que la règle est D(n) = 2n – 1.

Lors de ce projet, je peux vous garantir que les élèves ont réalisé, dans plusieurs cas, de très beaux jeux. Ces derniers sont devenus des décorations, comme certains jeux d’échecs, dans leur maison. Certains m’en reparlent lorsque je les croise en ville. Un projet qui a gravé des souvenirs dans leur mémoire. 

Quelques points clés pour l’activité :

  • Réserver le laboratoire de technologie de votre école ; 
  • Prévoir un budget et/ou utiliser des matériaux recyclés ;
  • Limiter les dimensions, par exemple, en ayant une base entrant dans un espace de 1 pied carré ;
  • Évaluer l’originalité du jeu. Le jeu peut être peint ou teint ;
  • Limiter le nombre de rondelles. Six est bien. 


Applications interdisciplinaires

Si le projet est mené dans un cadre interdisciplinaire, mentionner comment les mathématiques, l’art, les langues et l’histoire peuvent être intégrés ou liés dans ce projet. De plus, il s’agit d’un beau problème de critère B pour les élèves qui sont dans le programme d’éducation intermédiaire (PEI).

Partagez

Articles dans ce numéro

Se connecter