Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Pour une approche plus
simple de l’enseignement

des logarithmes

  • 14 minutes de lecture
Picture of Simon Méthot

Simon Méthot

Au moins une fois par décennie, mon meilleur ami m’appelle au téléphone pour me parler de sa haine des logarithmes. Comme nous sommes les deux dans la quarantaine, on doit s’en être parlé au moins cinq ou six fois. C’est un homme intelligent qui a fait des études poussées en finances. Les logarithmes sont un concept assez important dans ce domaine. Je me rappelle être allé avec lui et nos copines de l’époque au Céramik Café et son plan était de se faire une tasse avec toutes les lois des logarithmes pour s’aider dans ses devoirs universitaires. Aussi, pour tricher un peu dans ses examens. Disons que sa copine le trouvait vraiment ennuyeux ! 

Je me rappelle aussi avoir fait beaucoup de tutorat pour des jeunes qui avaient de la difficulté à comprendre les logarithmes. Quand j’ai eu la chance d’enseigner les mathématiques CST 4, en 2008-2009, et que la fonction exponentielle était au programme, je me suis dit que c’était ma chance de parler des logarithmes. Quelle ne fut pas ma déception de voir que la résolution se faisait par table de valeurs ou au moyen de la technologie et que le concept de logarithme n’était pas abordé. J’avais l’impression de tricher quand mes élèves cherchaient dix minutes en faisant des tables de valeurs et que, de mon côté, je pouvais résoudre les équations en dix secondes en utilisant des logarithmes. De plus, pour de simples résolutions comme celles faites en CST, je pensais que mes élèves pourraient facilement comprendre l’utilisation des logarithmes. 

Maintenant, le défi s’imposait de présenter ce concept aux élèves inscrits en CST 4. J’ai consulté quelques livres, des cahiers d’exercices et même certains sites web. Je n’ai rien trouvé qui me semblait assez simple ou en lien avec mes façons de procéder. J’avais l’impression qu’il fallait sortir de l’équation, faire un logarithme à part, et ensuite revenir au problème initial. Bref, je n’aimais pas du tout ce que je voyais.

 

Qu’est-ce qu’un logarithme ?

En cherchant rapidement sur internet, on trouve la définition suivante :

« Un logarithme est, en mathématiques, l’exposant auquel il faut élever une base donnée pour obtenir un nombre spécifique. En d’autres termes, c’est le nombre qui indique combien de fois la base doit être multipliée par elle-même pour atteindre le nombre donné. »

Cette définition vient de Gemini. Avant de me juger, demandez-vous ce que vos élèves vont regarder quand ils vont taper « logarithme » dans un moteur de recherche. Si on va sur le site de Alloprof, on retrouve l’identité suivante :

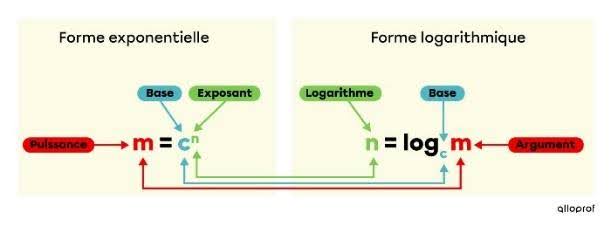
Figure 1

La définition de Gemini et l’image trouvée sur Alloprof sont toutes les deux correctes et efficaces. Cependant, je ne pense pas qu’elles aident à saisir vraiment l’essence des logarithmes et, surtout, comment les utiliser. Ce que je propose est une définition plus simple, qui, à mon avis, facilite grandement la compréhension des logarithmes, des lois qui les régissent, ainsi que leur utilisation.

 

Une couche de chaos

Enseignant maintenant en mathématiques SN 5, les élèves font un chapitre sur la fonction exponentielle et, ensuite, ils font un chapitre sur la fonction logarithmique. La résolution d’une équation exponentielle simple avec l’aide des logarithmes se fait avant l’étude complète des logarithmes et de la fonction logarithmique. Dans le but de compléter le chapitre sur la fonction exponentielle, nous n’avons pas le choix de parler des logarithmes. J’utilise une approche simple qui part de ce que les élèves connaissent et qui ajoute tout juste une simple couche de chaos sur la boule des savoirs mathématiques.

À force de jouer avec la couche de chaos, la boule redevient lisse, mais plus grosse. L’important est de bien attacher la couche de chaos à quelque chose qui est déjà bien acquis, mais qui fonctionne approximativement de la même façon. 

Pour introduire les logarithmes, je commence par les exercices fournis en annexe de cet article.

Prenons en exemple la question d).

25x x 125x = 78 125

On veut que l’élève réalise que les deux côtés de l’égalité ne sont pas dans la même base. Pour travailler avec les exposants, il faut absolument que les bases soient les mêmes. Tout le travail avec les logarithmes se construit sur le fait que l’on peut faire des changements de base.

On fait ces changements de base en utilisant les égalités fournies dans les tables de puissances de la question :

53 = 125,   52 = 25    et     57 = 78 125

On obtient :

(52)x (53)x = 57

Ensuite, on simplifie les exposants en utilisant les lois des exposants, vues en 3e secondaire: 

52x x 53x = 57

On veut qu’il y ait seulement une base de chaque côté de l’égalité. Ce qui donne :

52x+3x = 57

55x = 57

Comme les bases sont les mêmes, on peut alors dire que les exposants sont forcément égaux. On a donc accès à l’étage des exposants:

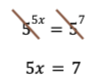
On peut ensuite trouver x. Une fois cette page d’exercices réalisée, on peut ajouter la couche de chaos.

 

Une définition simple

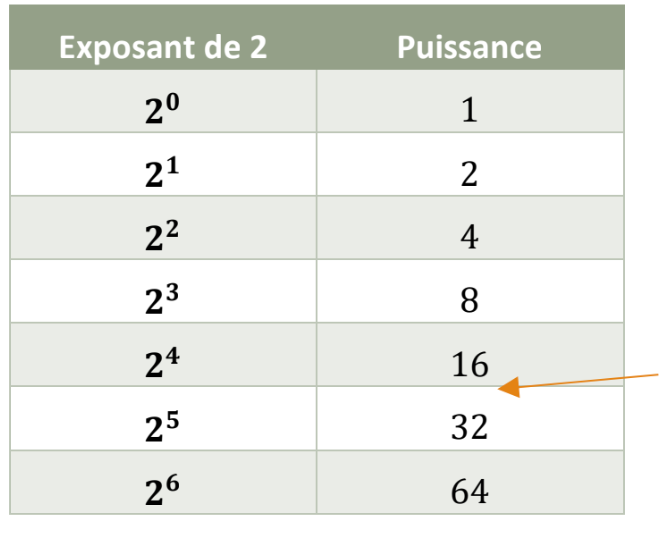
On repart avec la base 2 pour commencer, mais on pose une question qui tombe entre les valeurs fournies dans la table des puissances de 2. Prenons par exemple :

2x = 17

On sait que 24 = 16 et que 25 = 32. Le x doit être une valeur comprise entre 4 et 5. Il faut donc admettre ici notre ignorance et se tourner vers Dieu, ou la Sharp EL-W535XG. Ce qu’on cherche, c’est un exposant qui n’est pas arrangé avec le gars des vues.

C’est à ce moment que l’on peut parler du logarithme. Il faut que, la première fois que l’élève voit un logarithme en action, il soit placé à l’exposant. Parce qu’un logarithme, c’est un exposant. Comme il existe plusieurs bases et que l’on peut rechercher plusieurs nombres, il est important d’être précis. On indiquera dans le logarithme que la base voulue est 2 et que le nombre recherché est 17. Ce qui ressemble à ceci :

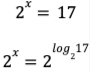
De cette façon, on voit qu’un logarithme, c’est tout simplement un exposant que l’on ne connaît pas. De plus, pour l’élève, le visuel est facile à comprendre et à retenir.

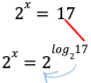
L’argument du logarithme est le nombre qui a été remplacé et la base du logarithme est la base utilisée dans l’égalité. Ensuite, comme la base est la même des deux côtés de l’égalité, on peut les simplifier et obtenir l’égalité suivante :

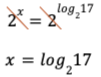
Ce qui revient à ce qui était présenté sur Netmath et aussi dans tous les manuels/cahiers d’exercices au Québec. Mais on y est arrivé sans passer par une identité, on a un visuel concret et, surtout, le logarithme a pris tout son sens.

 

Les lois des logarithmes ?

Comme un logarithme est tout simplement un exposant que l’on ne connaît pas, il va de soi que les lois des exposants s’appliquent aussi aux logarithmes. D’ailleurs, pourquoi les appeler les lois des logarithmes si ce sont les mêmes que les lois des exposants ? Pourquoi en faire un cas particulier ? J’aime bien dire à mes élèves que les lois des logarithmes sont en fait juste les lois des exposants en costume d’Halloween. Ce sont les mêmes lois, mais elles essaient de vous faire peur. L’Halloween est de loin la meilleure fête de l’année [1]. Regardons ensemble une de ces lois :

logcab = logc a + logcb

Quand je cherche des explications sur internet à propos des lois des logarithmes, les explications ne sont pas toujours très accessibles. Pourtant, les mathématiques sont censées être simples. Si l’élève a l’habitude de voir les logarithmes à la position des exposants, il pourra déduire cette loi par lui-même. En fonction du niveau de vos élèves, vous pouvez le faire symboliquement ou avec un exemple numérique :

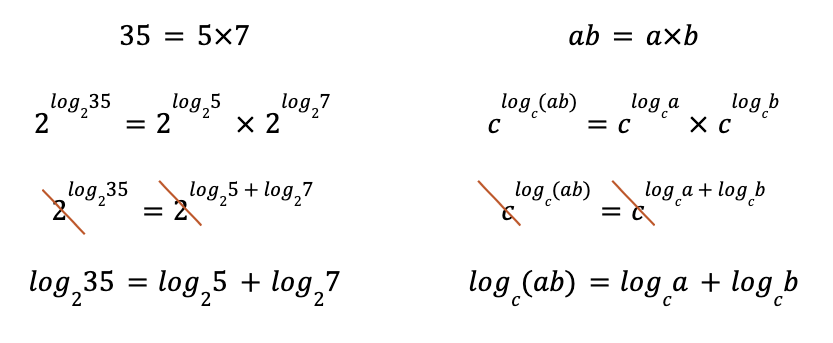
Grâce à cette façon de présenter les logarithmes, l’élève pourra facilement déduire le reste des lois des logarithmes. Il aura peut-être besoin d’un peu d’aide pour la loi du changement de base. Non pas parce que c’est trop difficile, mais surtout parce que l’élève n’en verra pas le besoin. La plupart des calculatrices scientifiques possèdent maintenant le bouton suivant (ou son équivalent) :

C’est ici que l’on peut, si le désir se fait sentir, entrer dans l’histoire des mathématiques et parler de John Napier (1550-1617) et des tables de logarithmes. Ou, dans l’histoire plus récente des mathématiques, où les calculatrices ne pouvaient que calculer des logarithmes en base 10 ou en base naturelle.

Reprenons le premier exemple de logarithme donné :

On pourrait demander aux élèves de transformer cette équation pour que la base soit 10 (ou e). On aurait l’équation suivante :

Grâce aux lois des exposants, on peut multiplier les exposants du terme de gauche de l’égalité et on obtient :

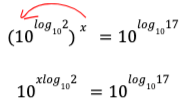
Comme les bases sont les mêmes des deux côtés de l’égalité, on peut les simplifier:

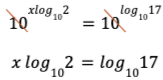
On isole x :

Cependant, dans le premier exemple de logarithme, on avait obtenu la valeur suivante pour x  :

Par transitivité de l’égalité, on a :

Ce qui est l’équivalent de la loi des changements de base :

Comme toutes les lois des logarithmes sont en fait des lois des exposants, est-il justifié de les classer à part ? N’est-il pas plus amusant d’imaginer des petites lois des exposants déguisées en petits loups ou en vampires ?

 

Les inéquations et les logarithmes

Les élèves ont souvent beaucoup de difficulté à savoir quand changer le symbole d’inégalité pendant la résolution algébrique d’une inéquation. Surtout si celle-ci contient des formes exponentielles ou logarithmiques. Soit l’inéquation suivante :

16 > 0,5x

Si on applique la méthode classique de l’enseignement des logarithmes, on obtient directement la réponse suivante :

x > log0,516

Mais comment choisir le bon signe autrement qu’en essayant des valeurs en x ou en traçant un graphique ? Avez-vous aussi remarqué que la variable x, qui était à droite dans la première inéquation, est maintenant à gauche dans les réponses ? C’est souvent ce qui arrive quand on enseigne les logarithmes de la façon traditionnelle. 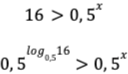Les élèves ont tendance à répéter ce qu’ils voient (souvent le soir avant l’examen quand il est rendu trop tard pour comprendre ce qui se passe ☹) et recopier bêtement les identités sans se poser de questions. Cela arrive souvent aussi avec la formule quadratique en 4e secondaire. Tout est beau quand on résout des équations, car le symbole d’égalité se lit dans les deux sens. Mais quand ce sont des inéquations, le symbole se lit de gauche à droite. Si l’élève a l’habitude de résoudre ce genre de question en plaçant son logarithme en exposant, il n’aura pas ce problème. Il économisera beaucoup de temps et évitera aussi quelques erreurs d’inattention.

La prochaine étape est de simplifier la base, mais, comme cette base est une valeur comprise entre 0 et 1 (exclusivement), il faut changer le symbole d’inégalité. 

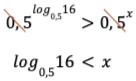
Je vous laisse le plaisir de vérifier. Vous remarquerez aussi que la variable x est restée du côté droit de l’inégalité, ce qui entraînera moins d’erreurs. L’élève a déjà vu que certaines valeurs associées à certaines opérations entraînent un changement de symbole d’inégalité. Quand on multiplie ou divise par un nombre négatif, quand on fait la variante négative d’une racine carrée, et là, on ajoute quand on simplifie des bases comprises entre 0 et 1. C’est tout. Pas besoin de vérifier des x ou de tracer un graphique. Je pense que l’économie de temps est non négligeable. On a seulement ajouté une opération dans la liste des opérations qui font inverser le symbole d’inégalité.

 

Pour se débarrasser d’un logarithme

Si la valeur recherchée dans une équation se trouve dans l’argument d’un logarithme, il faut simplement inverser le processus. En exemple :

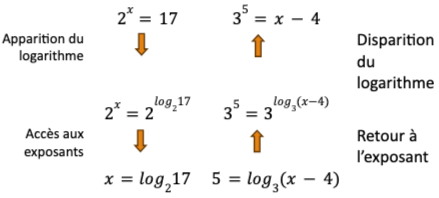
À gauche, le chemin emprunté jusqu’à maintenant dans la résolution d’équations exponentielles, et à droite, en partant du bas, on a le chemin inverse : une résolution d’équation contenant un logarithme. Comme un logarithme est tout simplement un exposant que l’on ne connaît pas, il faut le replacer à la bonne position. On veut donc l’écrire à l’exposant. La base choisie sera la même que celle utilisée dans le logarithme. 

Voici un autre exemple, mais qui se lit du haut vers le bas :

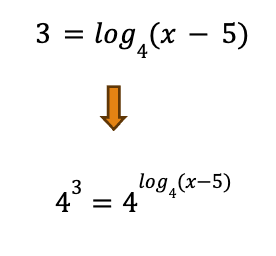
On replace le logarithme, qui est un exposant, à sa position. Le 3, qui est à gauche du symbole d’égalité, est aussi un exposant. On est sur le niveau des exposants. Le concept est le suivant :

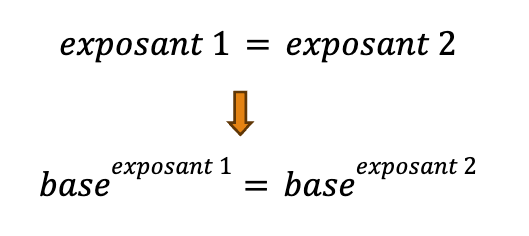
La base était 4. C’est indiqué subtilement dans le logarithme. C’est fou comme c’est bien pensé ! Ensuite, on évalue les deux côtés de l’égalité. À gauche, 43 vaut 64. À droite, la base 4 et le log4 sont des opérations inverses, elles se simplifient. Ce qui nous laisse seulement l’argument du logarithme sur la droite. On obtient :

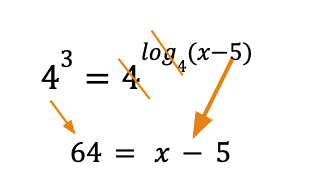
Ne reste plus qu’à continuer. Il est vraiment important que l’élève comprenne qu’un logarithme est tout simplement un exposant inconnu. Pour l’aider le plus possible dans cette compréhension, nous devrions toujours écrire le logarithme en exposant et ensuite simplifier avec la base. Oui, l’élève finira par développer des raccourcis, mais sa compréhension du concept sera grandement favorisée. De plus, la variable x restera du bon côté et le tout rendra la résolution d’inéquations plus facile.

 

Les inéquations et les logarithmes (prise 2)

Rendons-nous jusqu’au bout des choses : les inéquations contenant un logarithme. On fait la même chose que pour les équations, mais il faut se soucier des restrictions sur le domaine des logarithmes présents et savoir quand inverser le symbole d’inégalité. Sans surprise, il faudra le faire quand la base du logarithme sera un nombre compris entre 0 et 1. En gros, ça ressemblera à ceci :

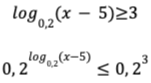
Comme la base était un nombre compris entre 0 et 1, il a fallu changer le symbole d’inégalité. On poursuit :

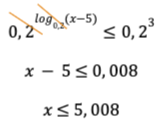
En incluant la restriction sur le logarithme, on arrive à la réponse suivante :

Je tiens à mentionner que je fais toujours tracer des croquis par les élèves les premières fois qu’on fait des inéquations. J’ai d’ailleurs toute une approche sur les graphiques des fonctions et sur le jeu des paramètres que je vous présenterai dans les prochains numéros de cette revue. Mais après quelques inéquations, on peut délaisser les croquis et résoudre les inéquations sans trop de soucis.

[1] Je suis prêt à en débattre!

Annexe

 

Voici un tableau des 10 premières puissances de 2, 3 et 5. Ce tableau vous aidera à compléter la question 1.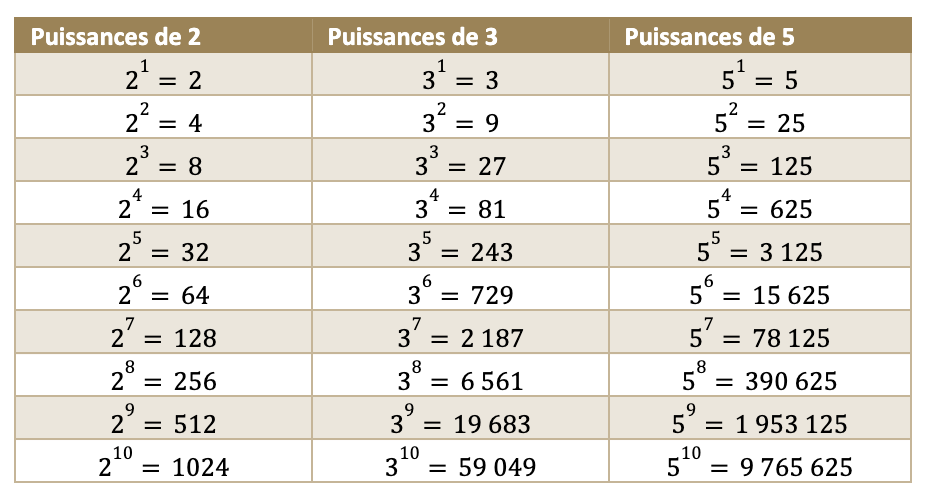

1. En utilisant le changement de base et les lois des exposants, résous les équations suivantes. N’oublie pas de valider tes réponses.
 
Partagez

Articles dans ce numéro

Se connecter