RÉCIT #3 D’UNE RECHERCHE-FORMATION À L’ENSEIGNEMENT DES PROBABILITÉS AVEC DES OUTILS TECHNOLOGIQUES :
Bouteille probabiliste
- 28 minutes de lecture

Mathieu Thibault
Je souhaite proposer les réflexions menées par 8 personnes qui ont participé à une recherche-formation à l’enseignement des probabilités avec des outils technologiques : 5 enseignant·es, 2 conseiller·ères pédagogiques et un chercheur- formateur (moi-même). Une recherche-formation vise à répondre à la fois à des intentions de recherche, pour contribuer à l’avancement des connaissances, puis à des intentions de formation pour les personnes qui y participent en quête de développement professionnel. Celle-ci a été menée dans le cadre d’une recherche doctorale (Thibault, 2021). Les cinq séances de formation se sont déroulées à intervalles réguliers sur une période d’environ sept mois. Cinq récits de formation de cinq à huit pages ont ainsi été rédigés (disponibles à l’annexe F de Thibault, 2021) par le chercheur-formateur après chacune des séances, puis envoyés aux participant·es en vue d’être discutés à la séance suivante. On y retrouve plusieurs exemples des réflexions et discussions qui ont émergé des séances. Plus précisément, ces récits de formation sont constitués d’un itinéraire des situations probabilistes abordées, des ressources qui les accompagnent (matériel, simulateurs, etc.) ainsi que des idées importantes qui ont émergé en séance.
Dans cet article, le troisième d’une série envisagée de 5 articles, je présente les réflexions associées à un récit de formation qui
a porté cette fois sur la situation de la bouteille probabiliste. On y retrouve les grandes idées évoquées lors de la séance de formation, notamment le potentiel, mais aussi les limites associées au recours de matériel de manipulation ainsi que d’un simulateur. On y retrouve aussi une réflexion sur les approches probabilistes (subjective, fréquentielle et théorique).
Bouteille probabiliste
Dans la recherche-formation, après avoir expérimenté la situation de Monty Hall (Thibault, 2023a) et la situation du jeu de dés (Thibault, 2023b), les participant·es ont expérimenté la situation de la bouteille probabiliste, dont l’énoncé est présenté dans l’encadré ci-dessous :
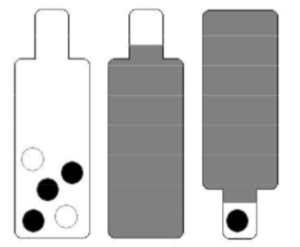 Vous avez une bouteille dont le contenu est caché. Vous savez qu’elle contient 5 billes de 2 couleurs différentes. On peut voir une seule bille à la fois, en retournant la bouteille.
Vous avez une bouteille dont le contenu est caché. Vous savez qu’elle contient 5 billes de 2 couleurs différentes. On peut voir une seule bille à la fois, en retournant la bouteille.
Comment émettre une prédiction sur le contenu de la bouteille ?
Analyse didactique de la situation
Cette situation est particulière puisqu’elle force l’entrée par l’approche fréquentielle, étant donné qu’on ne peut pas calculer la probabilité par l’approche théorique sans avoir accès au contenu de la bouteille. Il faut donc réaliser des essais pour émettre une prédiction (par l’approche subjective) quant au nombre de billes de chaque couleur dans la bouteille, puis mettre à l’épreuve cette prédiction en faisant ressortir une tendance dans les résultats. Cette situation favorise ainsi le développement de la pensée probabiliste et la prise de décision.
Il est à noter que les caractéristiques du contenu de la bouteille n’ont pas été choisies au hasard. En ayant cinq billes de deux couleurs différentes, il y a ici un choix réfléchi des variables didactiques. Parzysz (2019) joue sur ces variables didactiques en complexifiant la situation, alors qu’il a décidé de déposer dix-sept billes de trois couleurs différentes dans la bouteille et qu’il faut donc réaliser davantage d’essais pour être en mesure d’estimer avec confiance le nombre de billes de chaque couleur. Avec cinq billes de deux couleurs différentes, on sait qu’il y a entre une et quatre billes de chaque couleur.
Si après un nombre satisfaisant d’essais on obtient 63 % de billes rouges et 37 % de billes noires, on peut conclure qu’il devrait y avoir 3 billes rouges et 2 billes noires dans la bouteille. Étant donné la variabilité échantillonnale, il arrive parfois que la tendance ne soit pas aussi claire qu’on le souhaiterait, surtout s’il s’agit d’un échantillon d’un petit nombre d’essais. Plus particulièrement, si la fréquence d’une couleur de bille n’est pas près de 20 %, de 40 %, de 60 % ou de 80 %, on ne peut pas conclure avec confiance sur le nombre de billes de chaque couleur dans la bouteille.
Analyse didactique du simulateur
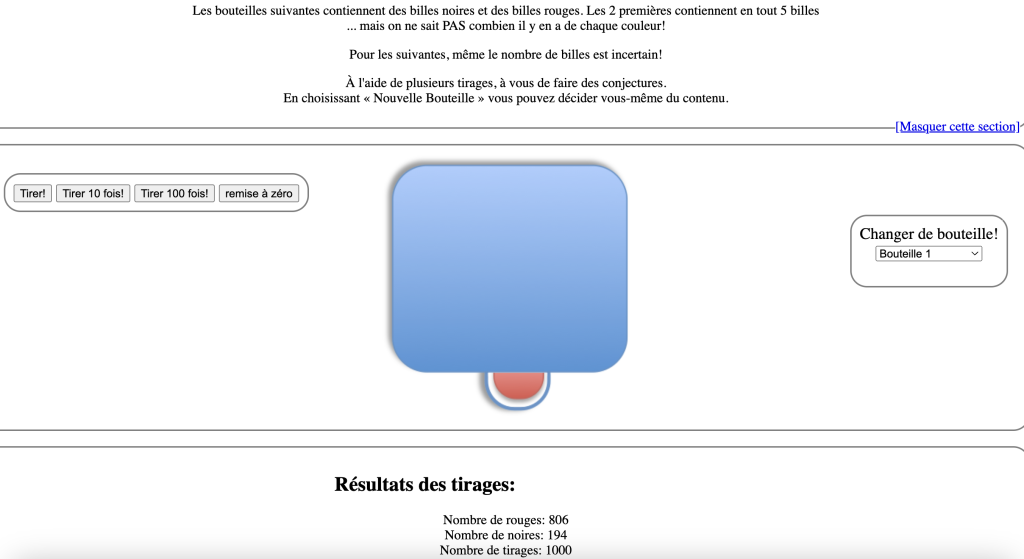
Comme l’indiquent les consignes du simulateur (Figure 1), on peut choisir une bouteille parmi quatre types de bouteilles (menu déroulant à droite), puis il faut tenter de trouver ce qu’elle contient en réalisant 1 essai à la fois (bouton « Tirer ! »), 10 essais à la fois (bouton « Tirer 10 fois ! ») ou 100 essais à la fois (bouton « Tirer 100 fois ! »), en recommençant les essais au besoin (bouton « remise à zéro »). Pour les deux premiers types de bouteilles, on sait qu’il y a cinq billes en tout comme dans l’énoncé de la situation. Ainsi, à partir des résultats illustrés, on peut estimer avec confiance que le premier type de bouteille contient 4 billes rouges ( 806 ÷ 1000 = 4 ÷ 5 ) et 1 bille noire (194 ÷ 1000 = 1 ÷ 5 ). Si on accède au programme du simulateur, on peut constater que la bouteille 1 « contient » 4 billes rouges et 1 bille noire, puis que la bouteille 2 « contient » 3 billes rouges et 2 billes noires. Un tel accès au contenu de la bouteille permet de calculer les probabilités, par l’approche théorique. Toutefois, les participant·es n’avaient pas accès au programme et ont dû se contenter des résultats des essais issus de l’approche fréquentielle pour estimer les probabilités.
Toujours selon les consignes du simulateur, on ne sait pas combien il y a de billes en tout dans le troisième type et le quatrième type de bouteille. Ce manque d’information amène à réfléchir selon le rapport entre les nombres de billes de différentes couleurs plutôt qu’un nombre de billes. Par exemple, si j’obtiens 500 billes rouges et 500 billes noires, je ne peux qu’affirmer qu’il semble y avoir autant de billes rouges que de billes noires, soit la moitié des billes au total, mais sans savoir s’il y en a 1 de chaque couleur, 2 de chaque couleur ou encore 500 de chaque couleur. Cette fois, si on accède au programme du simulateur, on peut constater que la bouteille 3 « contient » 1 bille rouge et 1 bille noire, puis que la bouteille 4 « contient » 4 billes rouges et 5 billes noires. À nouveau, les participant·es ne pouvaient pas calculer les probabilités par l’approche théorique et devaient plutôt se contenter des résultats des essais issus de l’approche fréquentielle.
De plus, l’option « Nouvelle Bouteille » du simulateur permet de décider combien de billes rouges et de billes noires contiendra la nouvelle bouteille, puis de réaliser des essais par la suite. Cette fonctionnalité offre la possibilité d’explorer des compositions extrêmes, par exemple 3 billes rouges et 10 000 billes noires. Cette option de choisir le contenu d’une nouvelle bouteille permet d’envisager de nouvelles questions qui changent la tâche.
Expérimentation avec les participant·es
Pour cette situation, les participant·es ont pu travailler en équipes de deux avec des bouteilles. Dès le départ, Christian (pseudonyme) a dit qu’on pourrait dévisser le bouchon de la bouteille pour regarder le nombre de billes de chaque couleur, ce qui est quelque chose que les élèves demandent habituellement. La contrainte de ne voir qu’une bille à la fois dans un tirage avec remise amène à adopter une approche fréquentielle plutôt que théorique, ainsi que d’avoir recours à l’approche subjective pour émettre des prédictions sur le contenu des bouteilles. Après quelques minutes, Christian s’est demandé si cela valait la peine de continuer à réaliser des essais, car il se disait qu’il y avait sûrement autre chose à faire (ou à calculer ?) pour répondre à la question.
Du côté de l’équipe d’Alan et Florence, après quelques essais réalisés avec une bouteille, Florence a demandé s’il y avait le même contenu dans chaque bouteille. Alan a alors précisé qu’il voulait savoir si tous réalisaient des essais avec le même contenu, mais il a ajouté qu’on le saurait au bout de 1 000 essais. Après une série d’essais, Alan a émis la prédiction qu’il y avait 1 ou 2 billes noires dans sa bouteille, car il a pigé environ 30 % de billes noires. Puisque cette fréquence était à mi-chemin entre 20 % et 40 %, il a constaté qu’il fallait réaliser davantage d’essais pour prendre une décision éclairée.
Après avoir obtenu plusieurs billes rouges consécutives, Brian a demandé s’il y avait bien deux couleurs dans sa bouteille et s’il s’agissait de billes de même taille. Il a finalement obtenu une bille noire après avoir pigé 18 billes rouges. Il en est donc venu rapidement à la prédiction que sa bouteille contenait 1 bille noire et 4 billes rouges. Déborah a alors fait remarquer qu’il n’y avait pas le même contenu dans sa bouteille que dans celle de Brian, car leurs résultats ne se ressemblaient pas. Les résultats obtenus par Brian étaient plutôt exceptionnels, mais j’y reviendrai dans le prochain article de la série, soit celui du quatrième récit de formation.
Après quelques minutes d’expérimentation avec les bouteilles, en tant que chercheur-formateur, j’ai proposé d’écrire avec quelle bouteille ils ont simulé: la bouteille beige ou la bouteille blanc et bleu. J’ai précisé que le contenu était le même dans les bouteilles de même couleur. Florence a demandé combien de temps il fallait pour réaliser les essais. J’ai répondu que l’on souhaite que les élèves posent cette question et que l’on veut les amener à réaliser qu’il faut effectuer le plus d’essais possible pour obtenir une tendance fiable. Ainsi, Grace a proposé de regrouper les résultats pour une même couleur. J’ai alors compilé les résultats de toutes les équipes pour les deux couleurs. Pour la bouteille blanc et bleu, nous avions obtenu, en tout, 116 billes rouges et 32 billes noires, soit environ 1/5 de billes noires, ce qui portait à croire qu’il y avait 1 bille noire et 4 billes rouges dans ce type de bouteille. Pour la bouteille beige, nous avions obtenu en tout 49 billes rouges et 48 billes noires, soit environ 1/2 de billes noires, ce qui était embêtant, car Grace a rappelé qu’il ne pouvait pas y avoir autant de billes rouges que de billes noires s’il y avait 5 billes dans la bouteille. Selon Christian, il faut continuer à réaliser des essais lorsque la tendance n’est pas claire. En effet, les résultats indiquaient un rapport 3:2, mais ce rapport pouvait aller dans un sens comme dans l’autre, étant donné que nous avions obtenu environ autant de billes noires que de rouges. Pour Christian, il y avait ainsi une double probabilité pour décider, dans l’idée qu’une probabilité permettrait de communiquer à quel point on est confiant de la probabilité qui est conjecturée.
Après quelques séries de 100 essais avec le simulateur pour les bouteilles 1 et 2, Brian a remarqué que cela correspondait aux résultats qu’il avait obtenus. De son côté, Alan était impressionné par la précision des résultats à long terme. Florence a ensuite demandé s’ils avaient été « chanceux » d’avoir une tendance claire avec peu d’essais, puis Alan a demandé à partir de quel nombre d’essais on peut considérer que la tendance est fiable. En tant que chercheur-formateur, j’ai précisé que chaque échantillon de 100 essais dans le deuxième type de bouteille n’est pas toujours de 60-40, mais que cela s’en rapproche tout de même. Donc, un échantillon de 100 est souvent suffisamment fiable, mais cela dépend aussi de la situation. Selon Déborah, un élève pourrait demander si le simulateur a été bien programmé et si on peut avoir confiance aux résultats qu’il produit. Il s’agit d’une remarque judicieuse, car le simulateur a un côté opaque, alors on ne sait pas avec certitude s’il a été bien programmé à moins d’avoir accès aux dessous de la programmation. J’y reviendrai plus particulièrement dans le cinquième récit de formation où il sera question de programmation de simulateur avec Scratch.
Concernant le matériel utilisé pour simuler cette situation, plusieurs participant·es ont remarqué qu’on pouvait voir les billes en regardant en dessous de la bouteille. Lorsque Déborah a demandé comment le matériel avait été produit, Grace a expliqué comment utiliser une bouteille d’eau et du ruban adhésif opaque en s’assurant qu’on ne peut voir qu’une seule bille à la fois à travers le goulot de la bouteille, sans pouvoir voir en dessous. Il y a différents types de bouteilles que l’on peut utiliser de manière à respecter ces deux contraintes (bouteille opaque et observation d’une seule bille à la fois). Par exemple, je me suis procuré au Dollarama des petites bouteilles opaques rouges et jaunes (ketchup et moutarde) ainsi que des mini « billes » de couleur, où chaque bouteille peut être identifiée avec un numéro pour garder une trace de ce qu’elle contient (Figure 2).

Figure 2.
Exemple de matériel pour les bouteilles probabilistes
Déborah a précisé qu’il est vraiment pertinent de réaliser des essais concrètement avant d’utiliser le simulateur. Brian a abondé dans ce sens, en mentionnant que les élèves vont davantage croire les résultats obtenus par le simulateur s’ils ont d’abord réalisé des essais avec de vraies bouteilles. Lors de la réalisation des essais, j’ai fait remarquer qu’il y avait plusieurs façons de noter les résultats et de se questionner sur l’importance (ou non) de l’ordre dans cette situation.
J’ai ensuite montré les bouteilles 3 et 4 du simulateur, où on ne connaît pas le nombre total de billes. Brian a affirmé avec raison qu’on ne connaîtra jamais le contenu exact de la bouteille, alors on doit fonctionner en termes de rapport. En fait, dans la bouteille 3, après avoir simulé 1 000 essais, nous avions obtenu 492 billes rouges et 508 billes noires. À partir de ces résultats, j’ai admis qu’on pourrait conclure qu’il y a une bille de chaque couleur, ou bien deux de chaque couleur… mais qu’il pourrait aussi y avoir 492 billes rouges et 508 billes noires. Alan a rétorqué qu’autant de billes ne peuvent pas entrer dans la bouteille. Mais comme il s’agit d’une bouteille virtuelle, une telle contrainte d’espace ne s’applique pas au simulateur. Pour une bouteille concrète (même de grande taille), cette contrainte serait pourtant bien réelle et Alan a précisé qu’une bouteille pleine ne permettrait pas à chaque bille d’être pigée puisque les billes ne pourraient pas circuler librement dans la bouteille.
Avec le simulateur, j’ai ensuite créé une nouvelle bouteille (Figure 3) en choisissant un contenu extrême, soit 3 billes rouges et 9 997 billes noires (ce qu’on pourrait difficilement faire concrètement). En réalisant des séries de 100 essais dans cette bouteille extrême, nous avons obtenu la première bille rouge après 5000 essais. Après 10 000 essais, nous en avions obtenu 3, conformément au contenu de la bouteille.

Figure 3. Résultats de 10 000 tirages avec une nouvelle bouteille
J’ai fait remarquer que les résultats vont varier, en raison de la variabilité échantillonnale, mais qu’on devrait habituellement avoir 1, 2, 3, 4 ou 5 billes rouges sur 10 000… mais pas 60 ! Brian a alors demandé si on pouvait en être certain et si la probabilité d’avoir 60 billes rouges était bel et bien nulle. Dans ces conditions, il n’est pas impossible d’obtenir 60 billes rouges après 10 000 essais, mais la probabilité de cet événement est excessivement faible. Brian a même affirmé qu’il pourrait passer sa vie à simuler des essais avec une telle bouteille et qu’il n’obtiendrait jamais 60 billes rouges en 10 000 essais dû à la rareté de cet événement. Déborah a ensuite demandé quelle question serait pertinente à poser avec la nouvelle bouteille du simulateur. La réponse à cette question n’était pas évidente pour les participant·es, car on veut que la pensée probabiliste soit mobilisée et on ne veut pas faire de cette situation un simple exercice de fractions équivalentes ou d’algèbre. Cela a amené Florence à s’interroger sur l’intention de cette fonctionnalité du simulateur. Grace était d’avis que ce simulateur serait efficace pour aider les élèves de deuxième secondaire à distinguer la probabilité théorique de la « probabilité fréquentielle » (expression utilisée dans des ressources québécoises, mais qui porte à confusion considérant que la probabilité est théorique en soi et que ce sont les fréquences qui sont empiriques, dans l’approche fréquentielle).
Dans un autre ordre d’idées, Alan a mentionné qu’au jeu de la roulette au casino, certaines personnes misent sur une douzaine si elle n’est pas sortie plusieurs fois d’affilée. En tant que chercheur-formateur, j’en ai profité pour parler de la conception de dépendance : dans un contexte du lancer d’une pièce de monnaie, même si on obtient pile 8 fois d’affilée, la pièce de monnaie n’a pas de mémoire… et donc chaque essai est indépendant des autres. Alan a rétorqué en affirmant que certaines personnes misent de cette façon, avec l’idée que la tendance va se rééquilibrer.
Dans la poursuite de cette discussion, Grace a amené le sujet des combinaisons à la Lotto 6/49. Christian a affirmé qu’il valait mieux ne pas prendre 1-2-3-4-5-6 au cas où cette combinaison sortirait, étant donné que le gros lot devrait alors être réparti parmi tous ceux qui l’ont choisie. En effet, j’ai ajouté que cette combinaison est habituellement celle choisie par des milliers de joueurs à chaque tirage de Lotto 6/49, car ils ne savent pas quoi prendre. Cette préférence de certains numéros pour former des combinaisons a d’ailleurs été analysée dans la revue Accromath (Delahaye, 2024). Grace était étonnée, car elle pensait que les gens seraient moins tentés à choisir la combinaison 1-2-3-4-5-6 étant donné qu’elle semble moins aléatoire. En fait, il s’agit de la conception de représentativité, où les personnes qui manifestent cette conception ont tendance à attribuer une probabilité plus
faible à un événement qui ne semble pas représentatif de ce que l’on obtient généralement. La combinaison 1-2-3-4- 5-6 peut sembler moins représentative des combinaisons tirées habituellement dans cette loterie, où les personnes qui manifestent la conception de représentativité peuvent croire (à tort) que la probabilité de l’obtenir est plus faible que pour une autre combinaison qui semble plus aléatoire (sans séquence logique). Alan en est donc arrivé à la conclusion qu’on devrait éviter de prendre cette combinaison à la Lotto 6/49. J’ai alors ajouté qu’il a raison, car la somme gagnée par un joueur sera moins importante s’il doit partager le gros lot avec un grand nombre d’autres personnes gagnantes (ce qui est confirmé par Delahaye, 2024)… et non pas parce que la probabilité d’obtenir la combinaison 1-2-3-4-5-6 serait plus faible que la probabilité d’autres combinaisons, ce qui n’est pas le cas. En effet, toutes les combinaisons de la Lotto 6/49 sont équiprobables, avec une probabilité de 1 ÷ 13 983 816, c’est-à-dire près 1 sur 14 millions (comme l’ont si bien dit les Cowboys Fringants dans une de leur chanson).
Réflexion sur les approches fréquentielle et théorique
Pour relancer les échanges, j’ai fait remarquer que les discussions précédentes autour de la situation de la bouteille probabiliste amènent à se demander ce que c’est de faire des probabilités. Aussi, j’ai demandé si cette situation devait être considérée de nature probabiliste ou statistique puisqu’elle ressemble à la démarche d’enquête statistique, soit de faire une hypothèse, de recueillir des données, de les organiser et de les interpréter pour répondre à la question. Selon Florence, tout est relié en mathématiques et cette situation aborde à la fois les probabilités et la statistique. Grace a précisé que la statistique montre une tendance du passé alors que c’est le futur pour les probabilités. En effet, lorsque l’on adopte une approche fréquentielle, on regarde les résultats du passé (statistiques) pour inférer le futur (probabilités). Cette inférence permet de connecter les probabilités et la statistique, dont l’articulation semble importante pour le développement conjoint des pensées probabiliste et statistique.
J’ai ensuite demandé si la priorité est accordée pour une approche probabiliste plutôt qu’une autre dans leur enseignement. Selon Grace, l’approche théorique prend plus de place actuellement dans les classes de mathématiques, ce qui concorde avec les résultats de l’enquête de Martin et al. (2021), où les personnes répondantes qui enseignent au secondaire (n = 388) ont dit recourir davantage à l’approche théorique qu’à l’approche fréquentielle, alors que c’est l’inverse au primaire (n = 237). Il est à noter que les enseignant·es ont peu (ou pas) été formés à l’enseignement des probabilités, particulièrement dans l’approche fréquentielle. Selon Déborah, l’enseignement des probabilités est généralement trop théorique et il est important de faire le lien avec ce qui est expérimental, par l’approche fréquentielle. Christian a ajouté que, s’il y a bien une partie des concepts et processus mathématiques qui peut être ludique pour les élèves, c’est en probabilités. Le recours à l’approche subjective en articulation avec les deux autres approches probabilistes permettrait aussi d’amener l’élève à émettre des prédictions, puis à les mettre à l’épreuve pour prendre des décisions éclairées.
Par la suite, Florence a mentionné humblement qu’elle n’a jamais été à l’aise en probabilités et qu’il s’agit de la seule section des mathématiques où elle se sent moins outillée, contrairement à l’algèbre par exemple. Ceci concorde avec les résultats de l’enquête de Martin et al. (2021), où les personnes répondantes qui enseignent les mathématiques au secondaire (n = 388) ont rapporté avoir un niveau d’aisance mathématique (comprendre les mathématiques pour soi) ainsi que de confiance didactique (enseigner les mathématiques aux élèves) significativement plus faible en probabilités par rapport aux autres domaines mathématiques. Déborah a dit qu’elle se sentait elle aussi démunie pour enseigner les probabilités, mais qu’une situation comme celle de la bouteille probabiliste peut l’aider. D’ailleurs, elle avait déjà entendu parler auparavant de cette situation, mais en ayant l’opportunité de l’expérimenter avec les bouteilles et avec le simulateur, elle a affirmé qu’elle pourra dorénavant aisément animer une période avec ses élèves à ce sujet. Selon elle, tant qu’elle n’a pas vécu une situation, c’est difficile de l’intégrer dans sa pratique. Florence a ajouté que c’est du temps à investir pour s’approprier de nouvelles situations, ce qui est souvent ce qui manque en enseignement, alors une occasion d’expérimenter une situation pourrait aider des personnes enseignantes à se sentir mieux outillées pour enseigner les probabilités. Déborah a conclu que cela fait partie d’un processus de changement de pratique et qu’elle a bien l’intention de se lancer dans le vide pour enseigner les probabilités avec cette situation.
C’est d’ailleurs ce que Déborah a fait dans les rencontres suivantes, en développant une séquence d’enseignement des probabilités en deuxième secondaire dans laquelle elle a intégré la situation de la bouteille probabiliste. Certains de ses élèves ont d’abord simulé 2 ou 3 fois des échantillons de 5 essais et étaient prêts à s’arrêter s’ils obtenaient le même résultat. Si les résultats des échantillons étaient différents, ils simulaient un peu plus d’essais. Déborah les a questionnés sur le nombre d’essais nécessaires, ce qui a incité les élèves à en réaliser plusieurs. Le simulateur de la bouteille a ensuite permis de réaliser un très grand nombre d’essais et les élèves ont compris qu’un grand nombre d’essais est important pour avoir une tendance fiable. Après cette activité d’introduction, Déborah voulait aller plus loin, car elle n’avait pas l’impression d’exploiter suffisamment les concepts probabilistes de deuxième secondaire. Elle a alors demandé à ses élèves de faire deux observations, en sachant qu’on a au moins une bille rouge et une bille noire dans chaque bouteille, pour se questionner sur ce qui pourrait être des événements possibles, soit RR, RN, NR, NN. Les élèves ont noté 20-30 fois les 2 essais, puis ils ont remarqué que RR était le résultat le plus fréquent et NN arrivait le moins souvent. Pourtant, quand Déborah leur avait demandé initialement la probabilité d’avoir RR sachant qu’il y a 4 possibilités, les élèves répondaient 1/4. Certains disaient aussi 1/5, car ils croyaient avoir 1 bille noire et 4 billes rouges dans leur bouteille. Puisqu’il n’y a pas de simulateur pour cette deuxième partie de l’activité, Déborah leur a proposé d’aller inscrire leurs résultats dans un tableur collaboratif, afin de compiler facilement les résultats. Lorsqu’est venu le temps de calculer les probabilités théoriques dans une autre activité, un groupe d’élèves a eu des résultats qui étaient très près de la probabilité théorique. Déborah était étonnée de voir que les élèves avaient mieux compris les concepts, comparativement à ceux des années précédentes. Dans l’intention de concevoir des diagrammes en arbre et de calculer des probabilités dans une situation d’un tirage (avec/ sans remise) de billes, les élèves ont utilisé un outil dynamique de diagramme en arbre sur GeoGebra (http://monurl.ca/ simulateur5) pour avancer à leur rythme et se corriger, donc dans un rôle de consolidation. Par exemple, ce diagramme en arbre permet de représenter le tirage sans remise de 2 billes d’un sac contenant 2 billes vertes, 3 billes bleues et 4 billes rouges, puis de faire ressortir les cas où on obtient au moins une bille rouge (Figure 4).
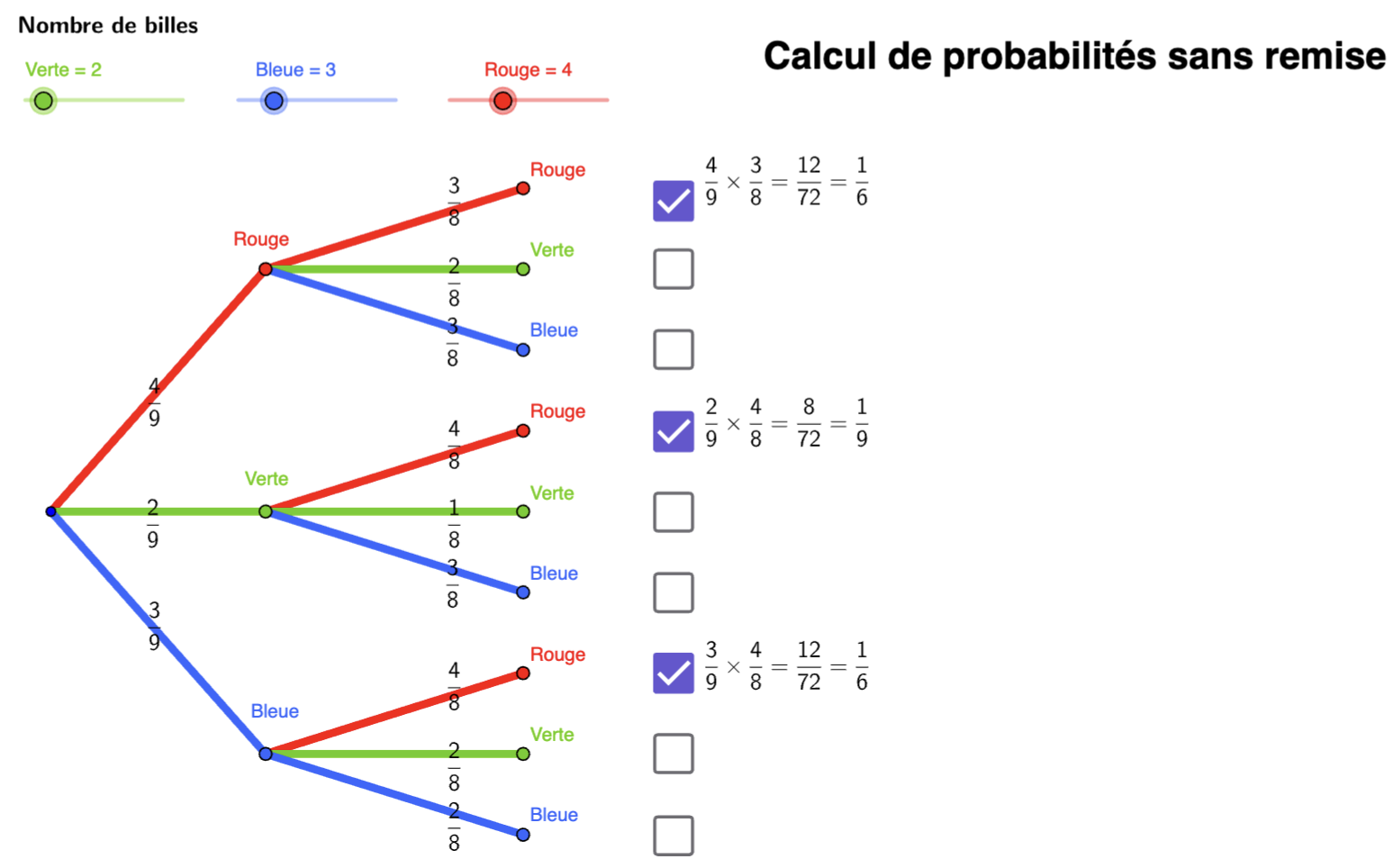
Figure 4. Diagramme en arbre dynamique sur Geogebra
Conclusion
Lors de la séance de formation, les participant·es ont expérimenté puis analysé la situation de la bouteille probabiliste, engendrant des discussions enrichissantes qui font ressortir l’importance de :
- Émettre des prédictions ;
- Expérimenter suffisamment d’essais (en se questionnant sur le nombre d’essais nécessaire) ;
- Regrouper les résultats pour que la tendance soit claire ;
- Utiliser du matériel de manipulation et des outils technologiques appropriés (en exerçant un jugement critique) ;
- Se questionner quant aux nouvelles questions que l’on peut se poser avec l’apport des outils technologiques, selon l’intention visée ;
- Être sensible aux conceptions probabilistes qui peuvent émerger en contexte de jeux de hasard et d’argent chez les élèves (et chez les enseignant·es) ;
- Donner à l’approche fréquentielle l’importance qui lui revient dans l’enseignement, en exploitant son côté ludique.
Il est à noter que d’autres outils technologiques peuvent être utilisés en lien avec la situation de la bouteille probabiliste. Pour l’approche fréquentielle, en plus du simulateur, on peut utiliser un tableur collaboratif (Google Sheets) qui offre des avenues intéressantes pour permettre une compilation interactive d’une grande quantité de données générées de manière collaborative. Pour l’approche théorique, le diagramme en arbre dynamique mentionné précédemment (http://monurl.ca/simulateur5) permet de faire ressortir des évènements composés et leur probabilité pour des tirages de billes sans remise.
En résumé, cette situation probabiliste captivante se révèle être pertinente tant pour la formation que pour l’enseignement au secondaire (ou même au primaire). En fait, elle fait partie du contenu que j’enseigne dans un cours universitaire de didactique des probabilités et de la statistique. J’avais élaboré une capsule vidéo (disponible à l’adresse https://monurl.ca/capsulebouteille, voir les 7 premières minutes) à des fins d’enseignement à distance. Cette capsule vidéo présente les étapes clés ainsi que les verbalisations qui peuvent être adaptées pour piloter une telle situation avec des élèves.
Et vous, seriez-vous prêts à intégrer une telle situation probabiliste dans votre enseignement ?
Références
- BRIAND, J. (2005). Une expérience statistique et une première approche des lois du hasard au lycée par une confrontation avec une machine simple. Recherches en didactique des mathématiques, 25(2), 247-282. https://halshs.archives-ouvertes.fr/halshs-00494923
- BROUSSEAU, G., BROUSSEAU, N. ET WARFIELD, V. (2002). An experiment on the teaching of statistics and probability. Journal of Mathematical Behavior, 20(3), 363-411. https://doi.org/10.1016/S0732-3123(02)00078-0
- DELAHAYE, J.-P. (2024). Solution du paradoxe «Gagner au loto». Accromath, 19, 42-43. https://accromath.uqam.ca/wp-content/uploads/2024/02/paradoxes_19_1.pdf
- MARTIN, V. ET MAI HUY, K. (2015). Une réflexion didactique sur des activités pour penser l’enseignement-apprentissage des probabilités et de la statistique à l’école primaire. Bulletin AMQ, LV(3), 50-67. https://www.amq.math.ca/wp-content/uploads/bulletin/vol55/no3/06-maitre-prob-et-stat-au-primaire.pdf
- MARTIN, V. ET THEIS, L. (2011). La résolution d’une situation-problème probabiliste en équipe hétérogène : le cas d’une élève à risque du primaire. Nouveaux cahiers de la recherche en éducation, 14(1), 49-69. https://doi.org/10.7202/1008843ar
- MARTIN, V., THIBAULT, M. ET ROY, N. (2021). Pratiques déclarées d’enseignement des probabilités : enquête auprès de personnes enseignantes du primaire et secondaire au Québec, Revue canadienne de l’enseignement des sciences, des mathématiques et de la technologie, 21(3), 596–624. https://www.researchgate.net/publication/355977386
- PARZYSZ, B. (2019). Des fréquences aux probabilités : apprendre à modéliser. Dans V. Martin, M. Thibault et L. Theis (dir.), Enseigner les premiers concepts de probabilités : un monde de possibilités ! (p. 43-70). Québec : Presses de l’Université du Québec.
- THIBAULT, M. (2021). Recherche-formation sur l’enseignement des probabilités du secondaire avec des outils technologiques : enjeux de formation. Thèse de doctorat. Université du Québec à Montréal. https://www.researchgate.net/publication/356145559
- THIBAULT, M. (2023a). Récit #1 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Monty Hall. Revue Envol, 181, 30-35. https://www.researchgate.net/publication/370320198
- THIBAULT, M. (2023b). Récit #2 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Jeu de dés. Revue Envol, 182, 6–11. https://www.researchgate.net/publication/374951685
- THIBAULT, M. ET MARTIN, V. (2016). Quand rien n’est certain, tout est possible : réflexion sur l’enseignement des probabilités. Revue Envol, 168, 16-21. https://www.researchgate.net/publication/309285996