- 3 minutes de lecture
Un défi mathématique pour tous les élèves du secondaire
Les Concours Opti-Math et Opti-Math+ sont organisés par un comité du GRMS et visent à encourager la pratique de la résolution de problèmes dans un esprit ludique et à démysti- fier, auprès des jeunes, les modes de pensée qui caractérisent la mathématique.
Voici des questions qui ont été sélectionnées parmi d’anciennes questions des Concours Opti-Math et Opti-Math+ du GRMS.
Opti-Math 1997
Situation 10
À la pêche
On a placé certains nombres entiers sur une droite numérique et on leur a demandé de nous donner des indices sur leur personnalité pour mieux les connaître.
- « Je suis un nombre carré, le nombre entier à ma gauche est un nombre cubique et celui à ma droite est un multiple de 5. »
Que vaut le carré du nombre décrit? - « Je suis moi-même la somme de trois nombres entiers consécutifs, le nombre entier à ma gauche est un nombre premier impair et celui à ma droite est un nombre carré. »
Que vaut le cube du nombre décrit? - « Je suis moi-même la somme de cinq entiers positifs consécutifs, le nombre à ma gauche est un nombre carré et celui à ma droite est divisible par trois. »
Quel sera le prochain nombre carré à la droite du nombre décrit?
Opti-Math 2003
Situation 13
La masse moyenne
Dans un groupe, il y a trois cents hommes de moins que le double du nombre de femmes.
La masse moyenne des hommes est de 73,2 kg et celle des femmes est de 60,8 kg.
La masse moyenne de toutes les personnes du groupe est de 63,9 kg.
Combien de personnes y a-t-il dans le groupe?
Opti-Math+ 2004
Situation 2
La cohabitation pacifique
Des biologistes ont observé le comportement de certaines sortes d’oiseaux. Il y en a qui cohabitent facilement alors que d’autres sont en perpétuel affrontement.
On a désigné 8 sortes d’oiseaux différents par les lettres A, B, C, D, E, F, G et H.
Le tableau ci-dessous présente les sortes d’oiseaux qui ne peuvent pas cohabiter entre eux.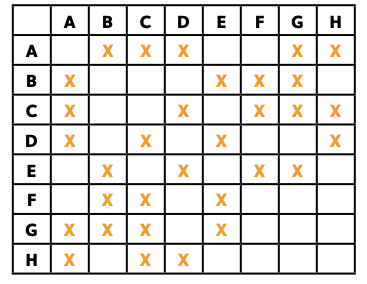
Il existe deux manières de placer trois sortes d’oiseaux pouvant cohabiter dans une même cage. Quelles sont ces deux manières?

Opti-Math+ 2010
Situation 7
Le bol à salade
Un bol à salade a la forme d’une pyramide droite tronquée à base carrée d’une hauteur de 24 cm.
Sa capacité est de 6,048 litres et le côté de sa grande base vaut le quadruple de celui de sa petite base.

Quelles sont les mesures de la grande base et de la petite base en cm? 1 litre équivaut à 1 000 cm3.