Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Le symbolisme en questions :

Le symbolisme
en questions :

le pourcentage

  • 16 minutes de lecture
Picture of Jérôme Proulx

Jérôme Proulx

Laboratoire Epistémologie et Activité Mathématique
Université du Québec à Montréal

Pourquoi le symbole % est-il utilisé pour dénoter un pourcentage? D’où vient-il? Que représente-t-il? Comme plusieurs symboles mathématiques, l’histoire du % n’est pas linéaire ni évidente. Elle est parsemée de coïncidences et d’événements fortement contextuels. Plusieurs raisons et événements ayant mené à l’écriture standard actuelle du pourcentage, soit %, sont fascinants, mais aussi assez curieux. Ce court article relate certaines de ces raisons et décrit quelques événements qui ont contribué à établir ce symbole dans le panorama mathématique actuel.

Première mise au point

Une première chose à dire sur le symbole de pourcentage est que, bien que commode pour aider à se rappeler du symbole lui-même, il n’y a pas de liens, historiquement, entre la forme du symbole %, avec sa barre et ses deux cercles, et la barre et les deux 0 du nombre 100. Ce qui suit permet de mieux comprendre son avènement — bien que le tout soit beaucoup plus nuancé et complexe qu’il n’est possible de l’expliquer ici. Tirée — et amalgamée — de différentes sources, l’histoire du symbole % ne doit pas être prise à la lettre, mais plutôt dans son ensemble évolutif à travers les bribes de documents historiques disponibles et les hypothèses diverses émises par différents savants de différentes époques.1

Premières origines

L’utilisation du concept de pourcentage semble tirer sa source des pratiques marchandes de taxes et d’impôts datant d’il y a très longtemps; certains les lient à des pratiques ayant eu cours plus de 2000 ans avant notre ère chez le peuple babylonien. Toutefois, ces taxes et impôts ne référaient pas à ce moment à la notion de 100, mais plutôt à des ratios variés relatifs aux biens qui étaient taxés. Par exemple, les autorités pouvaient percevoir une taxe à un fermier du type «Pour chaque trois balles de foin, une balle de foin est versée en taxes». Ce type de taxe a pu possiblement évoluer à travers les années pour devenir «Deux balles de foin par cinq produites», «1 par 6», etc., selon l’endroit ou encore le type de produit taxé (fruits, métaux, etc.). Toutes ces taxations étaient fortement ancrées dans une idée de ratio et de calculs de proportions. La base 100 pour ces ratios s’est tranquillement établie, par exemple en Inde et en Chine de 300 avant notre ère à 1100 après, mais sans raison explicite. Était-ce par facilité de calculs avec 100? Était-ce relatif à l’importance des montants se répartissant mieux par 100?

Pourquoi 100?

Le passage au «pour cent» n’est pas bien détaillé dans l’histoire, c’est-à-dire qu’il n’est pas si clair pourquoi 100 a été choisi comme base de comparaison pour ces calculs de ratios et plusieurs hypothèses coexistent. Certaines de ces hypothèses sont évidemment reliées à notre système de numération en base 10. Par contre, il n’est pas évident de comprendre pourquoi 100 est précisément le nombre choisi. D’autres hypothèses associent la place du 100 à l’émergence des systèmes d’argent et de monnaies, qui utilisent fréquemment les centimes, les sous, les cents, les dollars, etc. Toutefois, plusieurs de ces systèmes ont émergé bien après la notion de pourcent, rendant cette justification plus complexe. D’autres encore rattachent le 100 à des pratiques plus anciennes, par exemple aux taxations romaines de 1/100 perçues lors de certains échanges commerciaux. Finalement, d’autres, comme Baruk (1995), affirment tout simplement, en tenant pour acquis notre système de numération actuel en base 10, que c’est en fait le caractère raisonnable ou accessible du 100 qui en fait un choix privilégié, où 100 est vu comme étant un nombre qui n’est pas trop petit comme 10, mais pas trop gros non plus comme 1000. La question du 100 semble demeurer entière à ce jour, où d’autres nombres tels que 12, 50 ou 60 auraient pu remplir facilement les mêmes critères, tout en se référant à d’autres idées telles les heures, l’accessibilité, la divisibilité, les habitudes sociales, etc.

Quelles que soient les raisons expliquant la référence à 100, son utilisation dans les calculs de taxes et d’impôts n’était qu’une commodité, une façon de faire. En d’autres mots, le pourcentage comme concept n’existait pas vraiment à l’époque, pas au plan mathématique du moins, bien que des références à 100 parsemaient les calculs réalisés. En ce sens, l’idée de pourcentage n’était pas «représentée» en soi, elle n’était pas une chose à laquelle référer, mais semblait plutôt être une habitude calculatoire. Ainsi, sans concept de pourcentage, aucune symbolisation spécifique lui référant ne pouvait vraiment voir le jour, rendant par le fait même sa genèse un peu plus complexe à retracer. Par contre, c’est à force de transcrire ces habitudes calculatoires reliées à 100, et de vouloir informer des différentes techniques pour exécuter ces calculs (dans les livres de commerce, par exemple) que les choses ont pu évoluer au plan symbolique.

Partie-partie ou partie-tout?

Au-delà des questionnements sur l’origine du pourcentage, le fonctionnement lui-même des ponctions de taxes est flou. Lorsque la demande est de «1 panier de fruits pour 3 paniers produits», ce panier est-il un des trois produits ou un qui est supplémentaire aux trois? Il y a là la distinction faite en didactique des mathématiques entre une conception partie-tout (1 pour 3 revient à 1 des 3, donc 1 de donnée et 2 de conservées) et une partie-partie (1 pour 3 devient 1 des 4, donc 1 donnée et 3 conservées). Avec les pourcentages, cette distinction n’est pas toujours simple non plus. Dans la plupart des pays, les taxes sont en surplus des montants à payer et donc en mode partie-partie: un jean à 100$ avec 15% de taxe coûtera 115$ à l’acheteur. Au contraire, un impôt sur le revenu est plutôt traité en mode partie-tout: un salaire annuel de 100 000$ imposé à 25% impliquera que le contribuable conserve 75 000$ et donne 25 000$ au gouvernement. Ainsi, tel que le souligne Spiegelhalter (2019), dire 3% peut signifier autant 3|100, 3|97 ou encore 3|103, selon le contexte.

Manuscrits italiens

Divers manuscrits d’origine italienne reliés au commerce et datant des années 1400 sont considérés comme offrant les premières traces de symbolisation menant au symbole actuel de % pour représenter le pourcentage. Un élément à considérer est que ces manuscrits étaient souvent écrits ou annotés à la main. Ce détail, de prime abord anodin, semble avoir joué un rôle important sur le plan de la symbolique. En effet, la répétition constante, voire incessante, des mêmes mots peut mener à une certaine fatigue ou un empressement sur le plan calligraphique pour l’auteur. Ceci peut en retour mener à des manques dans la qualité de l’écriture ou tout simplement au développement d’abréviations pour des fins de rapidité d’exécution. Ainsi, l’expression «pour 100» en italien se dit per 100 ou encore per cento. Le per était souvent à l’écrit transformé en une sorte de P majuscule, séparant le nombre du 100, donnant P 100 ou P cento dans 7 P 100 ou 7 P cento. À l’occasion, ce cento a aussi été réduit à une sorte de «c» à tige allongée terminant en courbe pour représenter le «o» final de cento, un peu comme il est fréquent à l’écrit de terminer rapidement un mot en traçant une sorte de ligne (cette ligne servant même parfois à indiquer explicitement une certaine abréviation du mot). Par exemple, «légumes» à travers une liste d’épicerie peut souvent à la longue finir par passer de:
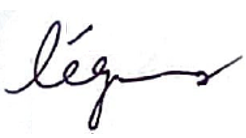àà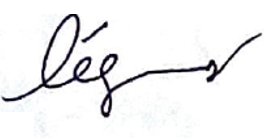

Et, ici, le contexte de «liste d’épicerie» aide à se rappeler ce qui est écrit et de son sens; alors que pris seul, un de ces gribouillis du mot «légumes» peut être difficile à déchiffrer. Un peu de la même façon, le cento, écrit rapidement et jumelé au P, pouvait donner des résultats du type suivant2:

ou

Pris dans un livre de commerce, et répété plusieurs fois par page ou même par paragraphe, cette graphie ne cause aucun problème. De plus, à force de répétition et de légères modifications, comme montré précédemment, une habitude d’écriture semble s’être graduellement installée. Il est possible de voir, dans ces divers manuscrits italiens, que la courbe de la fin du mot cento en vient tranquillement à être séparée de la «ligne de mot» et s’élever au-dessus de cette ligne, un peu de ces façons: ou

Ce petit rond, en haut à droite, semble aussi avoir pris un sens en relation avec les habitudes italiennes d’ordonner les nombres du premier , au deuxième , au troisième , etc. Ainsi, cento pouvait aussi devenir . L’écriture de per cento en est devenue de la forme  ou encore 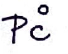, menant même lors des «fins de ligne» de texte, aux marges de la feuille, un condensé ou une imbrication du type .

Perceto, per cento ou per ceto?

Certains écrits historiques sur la notion de pourcentage ont parfois fait une coquille lorsqu’ils réfèrent à l’expression per cento: ils réfèrent plutôt par erreur à l’expression perceto. À l’écrit, à la main, la différence entre per cento et perceto est en effet assez subtile, où le «n» peut facilement être confondu. Curieusement, en Italien, perceto signifie «perçu», ce qui s’aligne assez bien au concept d’impôts et de taxes et donc aux pourcentages. Cette proximité entre per cento et perceto a aussi mené à une autre coquille, où le per et le ceto sont séparés pour donner per ceto. Ici, toutefois, cette expression se traduit en «par classe» et n’a plus vraiment de lien avec le concept de pourcentage. Ce jeu de coquilles est un bel exemple des surprises et richesses qui peuvent émerger autant du processus de traduction que de celui de transcription des écrits.

Les pratiques d’écritures sont évidemment variées et ont évolué, et le P de per semble aussi avoir pris différentes formes d’un manuscrit à l’autre, au point même d’avoir été délaissé à différents moments. Ceci a fait en sorte qu’à l’occasion uniquement, une référence à cento ait été conservée pour indiquer la procédure à suivre. Et, bien sûr, à travers les écrits à la main, la forme du a varié en hauteur et en longueur d’une transcription à l’autre, la courbe du «c» initial de cento pouvant devenir en forte proximité d’avec le petit rond (qui, tel qu’expliqué plus haut, peut être vu comme étant représentant de la numérotation ordonnée de centaine ou encore du « o » de cento).

Transformations diverses

La présence de plus en plus marquée non pas de mots et de nombres, mais d’une sorte de symbole se répétant d’un manuscrit à l’autre, a permis aussi implicitement de référer à cette procédure de «pour cent». Petit à petit, le concept s’est mis en place et les écrits s’y référaient explicitement: il n’était plus nouveau ou soudain de le voir apparaître, car il était de plus en plus utilisé dans le commerce. Bien évidemment, les symbolisations , ou co prises en elles-mêmes, sans les lier à leur évolution ou provenance, ne permettent pas aisément de retracer leurs origines au cento, au per, ni à la raison pour laquelle le petit rond est ajouté pour l’ordre ou la fin du mot cento. Cette coupure d’avec les origines de ces symbolisations ouvre en même temps la porte, ici aussi attribuable à l’écriture à la main, à des modifications, ajustements et contractions productives. Autour de 1650, les , ou co se sont lentement transformés, conservant une barre latérale et les deux «courbes» qui sont parfois elles-mêmes transformées en de simples points. De et , des symboles de la forme et commencent à faire implicitement leur entrée. Tel que souligné, le P de per est parfois présent, parfois difficile à lire ou encore simplement absent, où une certaine fusion entre le P et la courbe du «c» semble aussi avoir eu lieu pour donner des symboles tels que , , ou . Il y a alors ici une oscillation entre le rond et le point pour représenter chacun des deux cercles en haut et en bas de la barre. Avec la mise de côté du P de per, le symbole seul commence toutefois à s’établir de plus en plus pour représenter le calcul du pourcentage, par exemple avec 7 . Et, cette barre se voit devenir à l’occasion oblique dans les écrits, donnant le symbole % connu, pour écrire 7 %.

Standardisation et solidification du concept

Cette nouvelle écriture, soit le , mais surtout le % actuel, peut avoir été renforcée par ses liens avec la barre de fraction dans a/b, qui se voulait aussi une division. Ce lien avec l’écriture fractionnaire peut avoir joué un rôle important dans la standardisation de l’écriture % par les écrits et communications, où plusieurs éléments de différentes natures ont pu contribuer à cette solidification. Par exemple, l’écriture des fractions sous la forme a/b causait des problèmes techniques dans les transcriptions, car elle prenait plus de place qu’une simple ligne et s’étalait sur une partie de la ligne de texte sous elle. Cette écriture a donc été fréquemment substituée par l’écriture a/b qui s’écrivait sur une ligne simple sans altérer l’espacement des lignes écrites. De plus, l’avènement du symbole % coïncide assez bien avec les années où Leibniz tentait d’établir des symbolisations mathématiques plus standardisées dans les écrits mathématiques, en particulier avec les fractions, divisions, ratios et proportions (voir Cajori, 2019, pp. 180-195). L’écriture % s’alignait bien, par sa forme du moins, avec ces écritures de plus en plus prisées à l’époque.

L’écriture % s’établissant de plus en plus dans les écrits, le lien avec la barre et les deux zéros du 100 n’est pas passé inaperçu. Ce lien a eu aussi pour effet de renforcer la pertinence de cette symbolisation pour représenter les pourcentages, mais aussi d’en guider l’avènement d’autres symbolisations reliées. Ainsi, par analogie, le symbole ‰ pour représenter le ratio «per mil» a vu le jour, avec l’ajout d’un troisième zéro tel que retrouvé dans le nombre 1000. Autant cette nouvelle symbolisation ‰ a pris sa source dans le symbole %, autant elle a en retour encore plus justifié la pertinence du % pour représenter le pourcentage avec son lien avec 100.

Pourcent ou pourcentage?

En français comme en anglais, les mots pourcent, pourcentage, percent et percentage, sont souvent traités comme des synonymes. Leurs racines étymologiques et historiques sont évidemment connectées, mais le suffixe «-age» est surtout utilisé pour former un nom indiquant l’action de faire la chose, le processus à réaliser. Un peu comme avec jardin et jardinage, pourcentage signifie l’action de faire le pourcent. Par contre, leurs utilisations actuelles rend quelque peu floue leurs différences : pourcentage est très souvent associé à une chose (par exemple, un pourcentage comme résultat) et pourcent est fréquemment associé à un état à déterminer en insistant sur le «pour» (par exemple,  tant pour cent). Bien que certains auteurs aient tenté de les distinguer pour éviter les confusions, ces formes dans le discours courant sont maintenant bien installées. Malgré leurs amalgames, il est plus naturel d’entendre «30 pourcent» que «30 pourcentage» ou «pourcentage 30», et il est surtout question de l’étude des pourcentages  à l’école et non des pourcents. Selon le sens et le contexte, le choix semble se faire avec aisance.

Il est pertinent de porter attention à la transition de 100 vers «cent» en mots, ainsi que la contraction entre «pour» et «cent» donnant «pourcent». Ces transformations ont pu contribuer à la transition d’une action dans un calcul («tant pour 100» ou «tant pour cent») à une chose ou un concept, de «pourcent» auquel faire référence (calculer le pour cent) et même le désigner (un pourcentage). L’avènement d’un symbole, ici %, pour le représenter ne peut que participer à cette solidification en retour du pour cent en tant que concept mathématique lui-même. L’idée de s’intéresser de plus en plus au pourcentage comme concept, lié particulièrement à celle de «parties par centaine», a aussi eu comme influence de considérer d’autres ratios utiles du même type selon les contextes. En plus du «per mil», il y a aussi les notions de «parties par million», «parties par milliard», «parties par trillion», etc., qui ont autant leur source dans cette idée de pour cent qu’un symbolisme pour les représenter : ppm, ppb pour billions, ppt, etc. Encore ici, il y a la boucle du pourcentage qui donne naissance à d’autres concepts et ces concepts solidifient en retour la pertinence du pourcentage comme concept lui-même.

Dernières remarques

Voilà une certaine histoire du symbole %, bien comprimée et fortement synthétisée en quelques mots, un peu comme l’a subi la symbolisation du pour cent elle-même. Loin de devoir être prise à la lettre (ou au symbole !), cette histoire montre comment l’émergence de certains symboles n’est pas linéaire, mais aussi comment la symbolisation joue un rôle fondamental dans l’émergence du concept lui-même qu’elle tente de représenter. La forme et le contenu en mathématiques vont vraiment de pair…

[1] Les sources ayant influencé la suite sont variées, telles que Baruk (1995), Cajori (2012), Parker & Leinhardt (1995), et Smith (1970), en plus de différents dictionnaires étymologiques et historiques.
[2] Toutes les images d’écriture ont été reproduites à la main des textes originaux pour aider à les rendre plus lisibles.

Références

  • BARUK, S. (1995). Dictionnaire des mathématiques. Seuil.

  • CAJORI, F. (2012). A history of mathematical notations. Dover Publications.

  • PARKER, M., & LEINHARDT, G. (1995). Percent : A privileged proportion. Review of Educational Research, 65(4), 421-481.

  • SMITH, D.E. (1970). Rara Arithmetica (4e édition). Chelsea : NY.

  • SPIEGELHALTER, D. (2019). The art of statistics: learning from data. Pelican Books: R.-U.

Partagez

Articles dans ce numéro