Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Récit #4 d’une recherche-formation
à l’enseignement des probabilités
avec des outils technologiques:

Rondelles

  • 21 minutes de lecture
Picture of Mathieu Thibault

Mathieu Thibault

Professeur en didactique des mathématiques (UQO)

Mise en contexte

Je souhaite mettre de l’avant les réflexions menées par 8 personnes qui ont participé à une recherche-formation à l’enseignement des probabilités avec des outils technologiques: 5 enseignant·es, 2 conseiller·ères pédagogiques et un chercheur-formateur (moi-même). Une recherche-formation vise à répondre à la fois à des intentions de recherche, pour contribuer à l’avancement des connaissances, puis à des intentions de formation pour les personnes qui y participent en quête de développement professionnel. Celle-ci a été menée dans le cadre d’une recherche doctorale (Thibault, 2021). Les cinq séances de formation se sont déroulées à intervalles réguliers sur une période d’environ sept mois. Cinq récits de formation de cinq à huit pages ont ainsi été rédigés (disponibles à l’annexe F de Thibault, 2021) par le chercheur-formateur après chacune des séances, puis envoyés aux participant·es en vue d’être discutés à la séance suivante. On y retrouve plusieurs exemples des réflexions et discussions qui ont émergé des séances. Plus précisément, ces récits de formation sont constitués d’un itinéraire des situations probabilistes abordées, des ressources qui les accompagnent (matériel, simulateurs, etc.) ainsi que des idées importantes qui ont émergé en séance.

Dans cet article, le quatrième d’une série envisagée de cinq articles, je présente les réflexions associées à un récit de formation qui a porté cette fois sur la situation des rondelles. On y retrouve de grandes idées évoquées lors de la séance de formation, notamment l’analyse didactique de la situation et du simulateur ainsi que des réflexions issues de l’expérimentation avec les participant·es.

Situation des rondelles

Dans la recherche-formation, après avoir expérimenté les situations de Monty Hall (Thibault, 2023a), du jeu de dés (Thibault, 2023b) et de la bouteille probabiliste (Thibault, 2024), les participant·es ont expérimenté la situation des rondelles, dont l’énoncé est présenté dans l’encadré ci-dessous :

Une boîte contient trois rondelles de même format.Rondelles

  • La première rondelle est bleue sur ses deux faces.
  • La deuxième est rouge sur ses deux faces.
  • La troisième a une face bleue et une face rouge.

On brasse la boîte, on tire une rondelle au hasard, et on regarde une de ses faces seulement.

Le jeu consiste à prédire la couleur de l’autre face de cette rondelle.

Quelle stratégie optimiserait votre probabilité de gagner ?

Cette situation a déjà été traitée par quelques personnes autrices (Batanero et coll., 2010; Chernoff, 2019; Thibault, 2019 a, 2019 b; Venant et Thibault, 2019) et découle du paradoxe de Bertrand. Elle s’apparente à la situation de Monty Hall (Thibault, 2023a), alors qu’il faut déterminer la stratégie qui offre une meilleure probabilité de gagner et que cette situation est contre-intuitive elle aussi. Pour cette situation, une stratégie consiste à faire systématiquement son choix selon cette stratégie. Par exemple, une stratégie pourrait être de prédire que l’autre face sera toujours rouge, peu importe la face vue.

Pour réaliser cette situation, les participant·es, qui sont des enseignant·es et conseiller·ères pédagogiques d’expérience, ont travaillé en équipe de deux (comme on pourrait le faire dans une classe). Du matériel leur a été fourni, soit trois rondelles dans une boîte, comme dans l’énoncé de la situation. Il aurait aussi été possible (et plus économique) d’utiliser trois jetons de même couleur sur lesquels on pose des autocollants rouges et bleus, dans un sac de papier (figure 1).

Figure 1. Matériel

Figure 1. Matériel

Les participant·es ont pu explorer un simulateur de la situation des rondelles (monurl.ca/simulateur6), où on peut notamment réaliser un essai à la fois (figure 2).

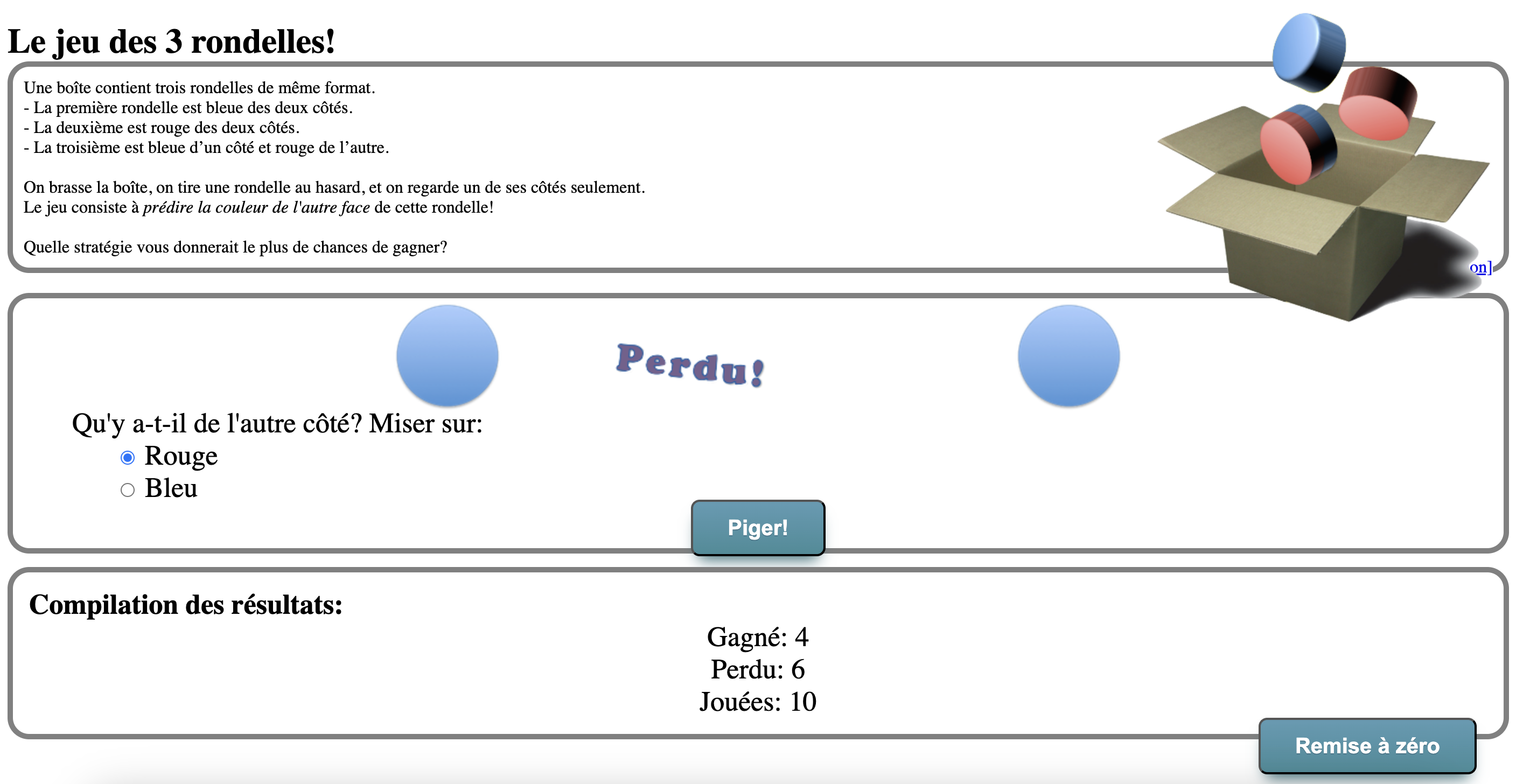
Figure 2 Résultats de 10 essais avec le simulateur (1 à la fois)

Après dix essais (un à la fois avec le bouton « Piger », puis « Vérifier »), la stratégie de toujours miser sur le rouge a permis de gagner six fois. Après avoir réalisé un certain nombre d’essais dans au moins deux stratégies différentes, les participant·es peuvent comparer plus systématiquement l’efficacité de toutes les stratégies. Pour ce faire, la fonctionnalité « Tester des stratégies » permet de simuler 100 essais pour une stratégie choisie. Voici un exemple de 100 résultats obtenus avec la stratégie « La couleur vue » du simulateur (figure 3).

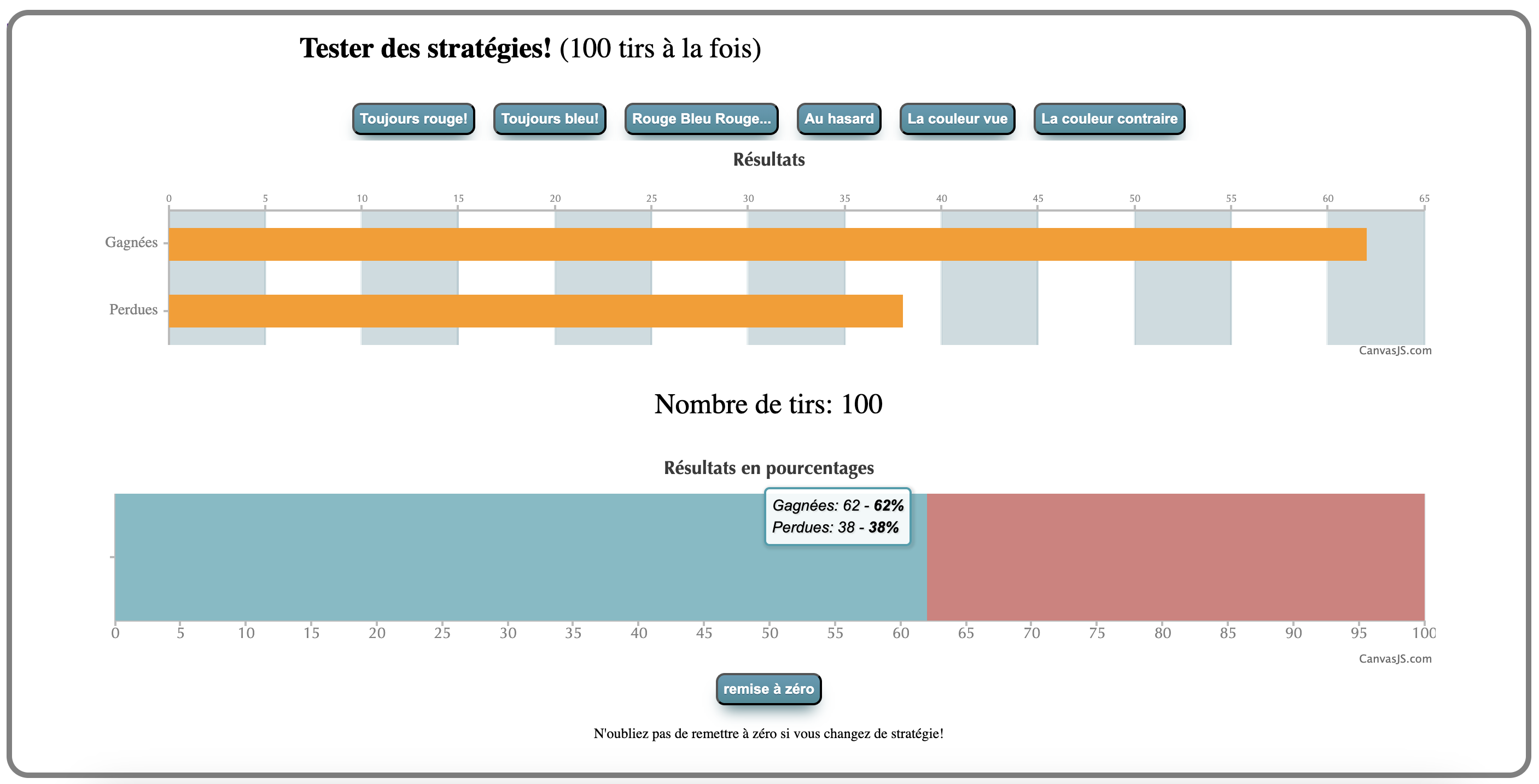
Simulateur 100 essais

Figure 3. Résultats de 100 essais avec le simulateur (100 à la fois)

Analyse didactique de la situation

Avant de réaliser des essais, il peut être intéressant que chaque participant·e fasse ressortir au moins deux stratégies possibles dans l’intention de comparer leur efficacité. Par l’approche subjective, on peut alors émettre une prédiction quant à la probabilité de gagner pour chacune d’elles. Une stratégie consiste à faire un choix de couleur systématique, selon la couleur de la face visible. Voici des stratégies qui peuvent émerger: 1)Toujours rouge; 2)Toujours bleu; 3)Alternance (rouge, bleu, rouge, bleu…); 4)Au hasard; 5)Couleur vue; 6)Autre couleur (que celle vue). Par exemple, en jouant avec la stratégie «Couleur vue», si on tire une rondelle dont la face vue est bleue, on prédira que la couleur de l’autre face sera bleue elle aussi.

Initialement, notre intuition peut porter à croire que les différentes stratégies amènent la même probabilité de gagner à ce jeu, soit  ½ mais ce n’est pas le cas. Puisqu’il s’agit d’une situation contre-intuitive, il y a un intérêt à expérimenter ce jeu par l’approche fréquentielle et ainsi constater que certaines stratégies n’ont pas une probabilité de gagner de ½. Ainsi, après avoir émis la prédiction qu’une stratégie serait optimale (ou qu’aucune n’est optimale), les participant·es peuvent réaliser des essais et ainsi expérimenter différentes stratégies pour mettre à l’épreuve leur prédiction. Les participant·es peuvent réaliser des essais avec le matériel fourni ou bien avec le simulateur de la situation des rondelles de façon similaire, soit un essai à la fois, ou encore en testant des stratégies avec des échantillons de 100 essais du simulateur.

Bien que les résultats du simulateur puissent amener à combattre une intuition erronée en provoquant un conflit cognitif, il reste toutefois à expliquer théoriquement la probabilité de gagner pour chaque stratégie. Par l’approche théorique, la stratégie «Couleur vue» est optimale, avec une probabilité de gagner de ⅔: si on voit une face bleue, la probabilité d’avoir tiré la rondelle bleu-bleu est deux fois plus élevée que la probabilité d’avoir tiré la rondelle bleu-rouge, étant donné que la première rondelle a deux faces bleues. En fait, parmi les trois faces bleues que l’on peut voir, deux d’entre elles ont une autre face bleue de l’autre côté (dans la rondelle bleu-bleu) et l’autre face qui est bleue a une face rouge sur son autre côté (dans la rondelle bleu-rouge). La probabilité d’obtenir la même couleur que celle vue est donc de ⅔ et, de façon complémentaire, la probabilité d’obtenir une couleur différente de celle vue est de ⅓. Ce diagramme en arbre (provenant de Thibault, 2019b, p. 184) permet alors de représenter tous les cas possibles (figure 4).

Bien que les résultats du simulateur puissent amener à combattre une intuition erronée en provoquant un conflit cognitif, il reste toutefois à expliquer théoriquement la probabilité de gagner pour chaque stratégie. Par l’approche théorique, la stratégie «Couleur vue» est optimale, avec une probabilité de gagner de: si on voit une face bleue, la probabilité d’avoir tiré la rondelle bleu-bleu est deux fois plus élevée que la probabilité d’avoir tiré la rondelle bleu-rouge, étant donné que la première rondelle a deux faces bleues. En fait, parmi les trois faces bleues que l’on peut voir, deux d’entre elles ont une autre face bleue de l’autre côté (dans la rondelle bleu-bleu) et l’autre face qui est bleue a une face rouge sur son autre côté (dans la rondelle bleu-rouge). La probabilité d’obtenir la même couleur que celle vue est donc de  et, de façon complémentaire, la probabilité d’obtenir une couleur différente de celle vue est de ⅓. Ce diagramme en arbre (provenant de Thibault, 2019b, p. 184) permet alors de représenter tous les cas possibles (figure 4).

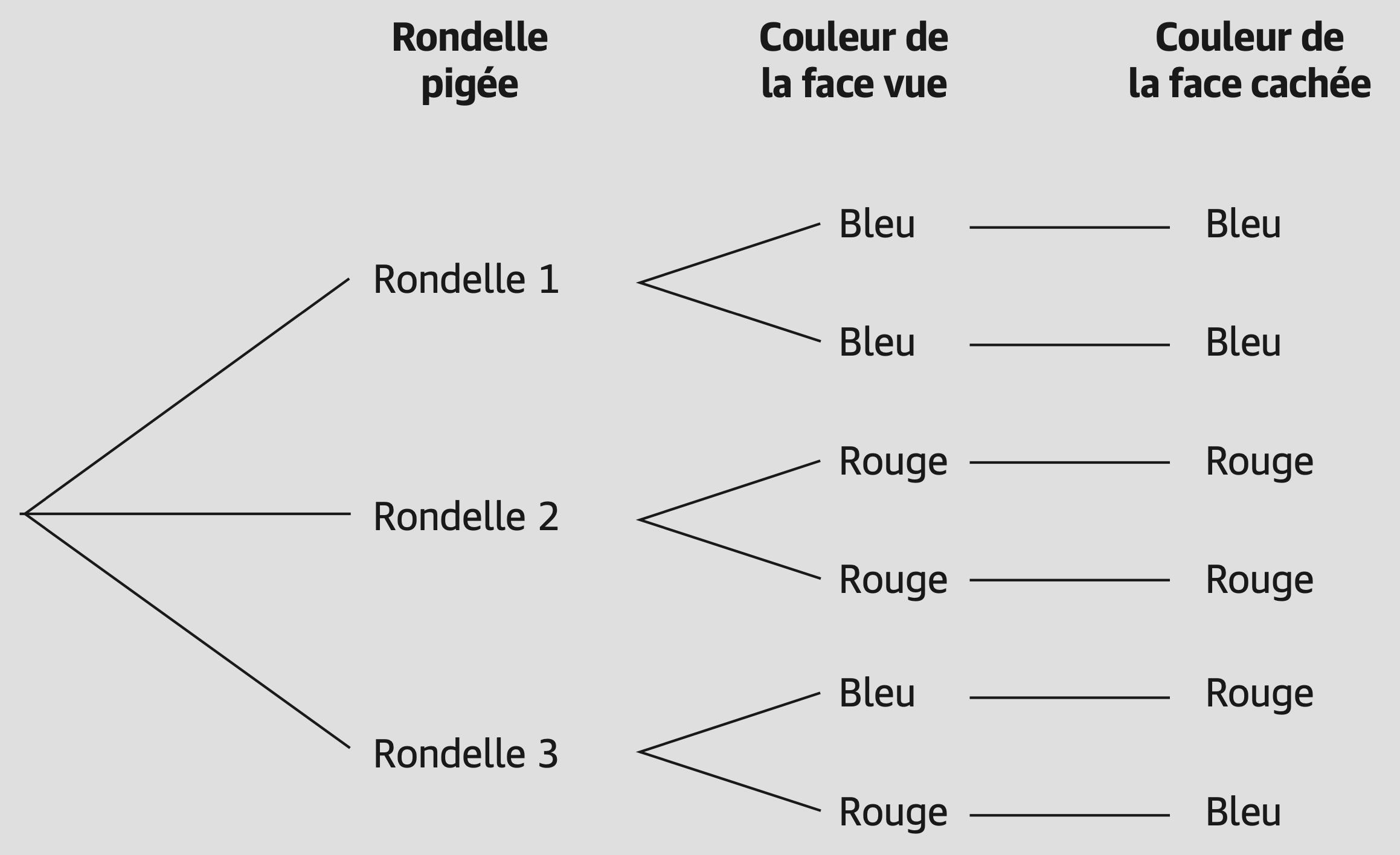
Diagramme en arbre

Figure 4. Diagramme en arbre de la situation des rondelles (Thibault, 2019b, p.164)

La particularité de ce diagramme en arbre est que la dernière étape, soit la couleur de la face cachée, est complètement déterminée: si on est avec la rondelle 1 (bleu-bleu) et qu’on voit une face bleue, il est certain que l’autre face sera bleue aussi. En adoptant un raisonnement théorique à partir des rondelles dans le diagramme en arbre, étant donné que deux des trois rondelles ont la même couleur sur chacune des faces, il est préférable de prédire que l’autre face sera de la même couleur (probabilité de ⅔) plutôt que de couleur contraire (probabilité de ⅓). De façon similaire, en raisonnant plutôt à partir des faces, il y a six cas possibles (les six faces des trois rondelles), dont quatre qui permettent de gagner en prédisant la couleur vue, puis deux qui permettent de gagner en prédisant la couleur contraire.

Dans ce jeu des rondelles, ce que l’on veut tester n’est pas seulement le jeu lui-même, mais particulièrement l’efficacité de stratégies appliquées à ce jeu. Il ne s’agit donc pas seulement de rechercher la probabilité de gagner, mais de définir un ensemble de stratégies puis, parmi celles-ci, de chercher celle qui procure la probabilité la plus élevée de gagner. Cette situation contre-intuitive favorise ainsi le développement de la pensée probabiliste et la prise de décision.

Analyse didactique du simulateur

Lorsqu’on utilise le simulateur un essai à la fois, il est possible de changer de stratégie d’un essai à l’autre, ce qui viendrait biaiser les résultats qui seraient compilés. En effet, en regroupant les résultats de différentes stratégies, il n’est plus possible de déterminer la probabilité de gagner pour chacune d’elles. Il est alors préférable d’expérimenter séparément chaque stratégie, en réinitialisant les résultats (à l’aide du bouton «Remise à zéro») avant d’en expérimenter une autre. Le simulateur peut aussi être utilisé pour tester des stratégies (100 essais à la fois). À nouveau, sachant qu’on peut regrouper des résultats seulement s’ils sont générés dans les mêmes conditions, il est nécessaire de réinitialiser les résultats chaque fois que l’on change de stratégie, comme l’indique la note en petits caractères («N’oubliez pas de remettre le simulateur à zéro si vous changez de stratégie»).

Cette fonctionnalité du simulateur de tester des stratégies permet d’observer le dynamisme dans les résultats, en regardant l’évolution des pourcentages lors de la simulation dynamique d’un échantillon de 100 essais. Du coup, ce simulateur permet de donner du sens à des notions probabilistes, notamment en permettant de visualiser la Loi des grands nombres par une stabilisation à long terme des fréquences. D’autres rôles du simulateur ont déjà été abordés dans un autre texte (Thibault, 2019b), par exemple d’illustrer les résultats des essais à l’aide de diverses représentations.

Expérimentation avec les participant·es

Lorsque la situation des rondelles a été expérimentée avec les participant·es de la recherche-formation, le chercheur-formateur (moi-même) a donné accès à la mise en situation, au simulateur et au matériel.

Dans l’équipe de Grace et Brian (pseudonymes), ce dernier pensait initialement qu’aucune stratégie ne pourrait l’aider à gagner plus fréquemment, mais Grace lui propose tout de même d’en tester deux, en commençant par la stratégie «Toujours bleu». Après quelques essais réalisés avec le matériel, Brian a remarqué que la stratégie «Toujours bleu» (6 gains sur 10 essais) leur a permis de gagner plus fréquemment que la stratégie «Alternance» (2 gains sur 10 essais). Selon lui, ces résultats sont dus au fait qu’il a souvent pigé la rondelle bleu-bleu. Grace et Brian ont toutefois admis que 10 essais ne sont pas suffisants pour prendre une décision éclairée. Brian a de nouveau répété qu’aucune stratégie ne l’aiderait à gagner plus fréquemment et Grace était d’avis que les stratégies devraient offrir une probabilité de gagner de «50-50». En utilisant le simulateur, Brian a compris avec conviction que l’efficacité d’une stratégie se démarque des autres, en voyant bien les résultats autour de ⅔ pour la stratégie «Couleur vue». Grace a alors fait remarquer que la rondelle rouge-rouge est éliminée si on voit une face bleue: il y a alors 3 autres faces possibles en voyant bleu (soit rouge, bleu et bleu), ce qui explique la probabilité de ⅔.

Du côté de l’équipe de Émilie et Déborah, chacune souhaitait adopter une approche différente. Déborah voulait naturellement procéder par l’approche théorique en calculant les probabilités alors qu’Émilie souhaitait plutôt avoir recours à l’approche fréquentielle en réalisant des essais. Elles se sont entendues pour commencer de manière expérimentale, sans choisir de stratégie initialement. Après quelques essais réalisés avec le matériel, elles ont constaté qu’il est préférable de choisir la stratégie de la «Couleur vue» (7 gains sur 11 essais) que de choisir la stratégie de l’«Autre couleur» (4 gains sur 11 essais), mais en admettant qu’il faudrait réaliser plus d’essais pour conclure. De façon théorique, elles ont ensuite calculé qu’il y a 6 cas possibles dont 4 qui permettent de gagner en gardant la couleur et 2 en changeant de couleur. Déborah a alors construit un arbre de probabilités (similaire à celui présenté précédemment), en s’appuyant sur les 6 faces pour les 3 rondelles. Déborah a alors constaté que les stratégies Toujours bleu et Toujours rouge ont une probabilité de gagner de 50 %.

Selon Grace, les élèves pourraient d’abord émettre une prédiction de probabilité pour chaque stratégie avant de réaliser des essais. Pour les élèves qui pensent intuitivement que chaque stratégie a une probabilité de 50 %, elle a proposé de leur dire qu’il y a une stratégie qui fait gagner plus fréquemment que les autres, afin de provoquer un conflit cognitif et les remettre à la tâche pour trouver de quelle stratégie il s’agit.

En ce qui concerne l’utilisation du simulateur pour tester des stratégies, Grace a aimé voir les diverses stratégies qui sont proposées où certaines sont vraiment différentes. Grace a toutefois suggéré de demander d’abord aux élèves de faire ressortir différentes stratégies avant de voir celles du simulateur. Il a aussi été mentionné que, si on s’arrête aux quatre premières stratégies (Toujours rouge, Toujours bleu, Alternance, Au hasard), la conception que toutes les stratégies ont une probabilité de gagner de 50 % pourrait être renforcée. Pour éviter cela, le chercheur-formateur a proposé de faire comparer une stratégie parmi les quatre premières, puis une autre parmi les deux dernières (Couleur vue, Autre couleur) pour constater que les probabilités ne sont pas toutes les mêmes. Selon Brian, les résultats du simulateur étaient convaincants, car il a simulé quelques centaines d’essais pour constater que cela tendait vers ⅓ et non pas 50 % comme il le croyait intuitivement.

À l’aide du simulateur, Émilie a réalisé des échantillons de 100 essais pour la stratégie «Toujours rouge». Après 13 échantillons de 100 essais, elle a remarqué que cette stratégie avait permis de gagner à plus de 50 % dans 8 des 13 échantillons. Ce constat a amené le chercheur-formateur à questionner si la face rouge arrive plus souvent que la face bleue. Il a alors demandé si la fréquence de face rouge était vraiment supérieure à 50 % si on cumulait tous les essais. En effet, le cumul des 13 échantillons devrait être plus stable que chaque échantillon pris séparément, tout en admettant que la variabilité demeure dans une expérience aléatoire. Dans le cas de ces 1 300 essais, les résultats n’étaient finalement pas vraiment exceptionnels, car ils ne sortaient pas tellement de l’ordinaire.

Pour sa part, Déborah s’est intéressée au dynamisme des résultats, en regardant l’évolution des pourcentages lors de la simulation dynamique d’un échantillon de 100 essais avec la stratégie «Toujours rouge». Elle a remarqué que, parfois, la fréquence ne croise jamais le 50 %, car cela oscille entre 42 % et 48 % par exemple. En testant 3 fois des échantillons de 100 essais en groupe avec le simulateur, le chercheur-formateur a obtenu 2 fois une fréquence exacte de 50 % (figure 5), ce qui est apparu comme très peu probable. Ces résultats ont fait réagir les participant·es, notamment Émilie qui avait eu de son côté une fréquence exacte de 50 % une seule fois sur 13 échantillons de 100 essais.

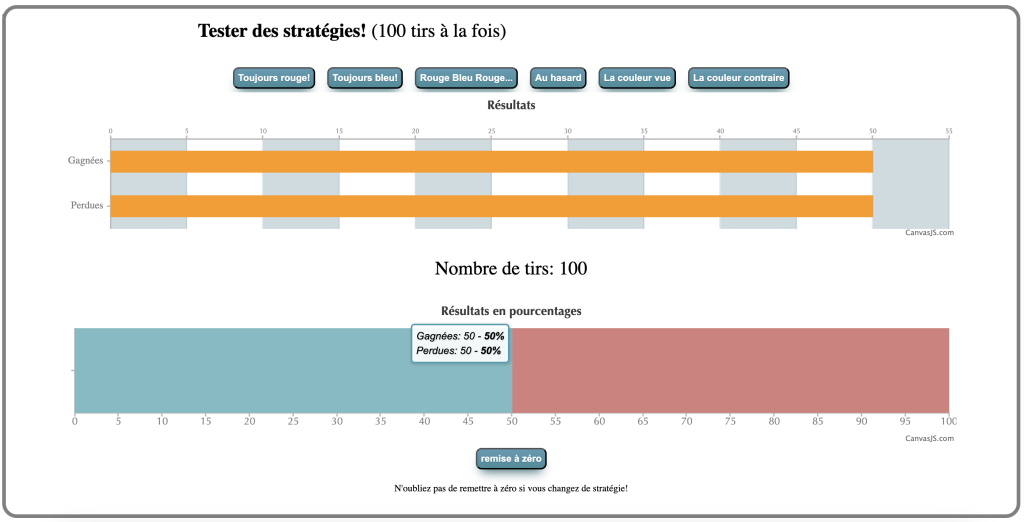
Fréquence de 50%

Figure 5. Fréquence de 50 % obtenue avec le simulateur pour la stratégie «Toujours rouge»

Il convient de préciser que la stratégie « Toujours rouge » de la situation des rondelles offre une probabilité de gagner de 50 %, ce qui ne garantit toutefois pas d’obtenir exactement 50 gains en 100 parties. En fait, il est peu probable (probabilité calculée d’environ 8 %) de gagner exactement 50 fois dans ces conditions, ce qui semble cohérent avec les résultats d’Émilie, qui a obtenu exactement 50 gains une seule fois sur 13 échantillons de 100 parties. Donc, s’il est peu probable d’obtenir cet évènement une fois, il est encore moins probable de l’obtenir deux fois en trois reprises. Les participant·es se sont donc demandé si ces résultats étaient exceptionnels, au sens où ce sont des exceptions un peu inattendues. À la suite de cette séance de formation, le chercheur-formateur a effectué des calculs plus avancés pour déterminer qu’il s’agissait d’un résultat exceptionnel (probabilité d’environ 0,6 %). Le chercheur-formateur a d’ailleurs précisé aux participant·es qu’il s’agissait d’un cas rare puisque, par convention, le seuil significatif est habituellement fixé à 5 %. Ce seuil permet de désigner la frontière entre des résultats attendus et des résultats inattendus, où les variations ne seraient probablement pas attribuables au hasard. Ce résultat exceptionnel a amené les participant·es à être encore plus attentifs à d’éventuels résultats exceptionnels provenant d’essais réalisés dans l’approche fréquentielle. Certaines personnes participantes, dont Émilie, ont même développé une sensibilité aux résultats exceptionnels, alors qu’elles se sont demandé à divers moments ultérieurs si certains résultats obtenus par l’approche fréquentielle sortaient de l’ordinaire.

L’utilisation d’un simulateur pour générer les résultats d’un grand nombre d’échantillons de 100 essais permet d’observer à l’occasion des résultats exceptionnels. En effet, on peut obtenir plus facilement des résultats exceptionnels avec le simulateur, car on peut générer quasi instantanément les résultats de nombreux échantillons d’essais. En d’autres mots, le simulateur permet de générer des résultats exceptionnels de façon plus rapide, mais non pas de façon plus fréquente (au sens proportionnel).

Conclusion

Lors de la séance de formation, les participant·es ont expérimenté puis analysé la situation des rondelles, engendrant des discussions enrichissantes qui font ressortir l’importance de :

  • Faire ressortir les différentes stratégies possibles ;
  • Émettre une prédiction quant à la probabilité de gagner pour chaque stratégie (approche subjective) ;
  • Utiliser du matériel de manipulation et des outils technologiques appropriés (en exerçant un jugement critique) ;
  • Tester deux stratégies (qui ont des probabilités de gagner différentes) ;
  • Réaliser des essais à l’aide de matériel, puis noter les résultats (approche fréquentielle) ;
  • Compiler les résultats et revenir aux prédictions initiales ;
  • Utiliser le simulateur pour tester plus efficacement les six stratégies ;
  • Expliquer les probabilités théoriques de gagner avec chaque stratégie avec un diagramme en arbre (approche théorique) ;
  • Utiliser le simulateur pour observer le dynamisme des résultats et pour questionner si le rouge arrive plus souvent que le bleu ;
  • Être à l’affût de résultats exceptionnels obtenus par l’approche fréquentielle.

En conclusion, cette situation probabiliste étonnante se révèle être pertinente tant pour la formation que pour l’enseignement au secondaire (ou même au primaire). En fait, elle fait partie du contenu que j’enseigne dans un cours universitaire de didactique des probabilités et de la statistique. J’avais élaboré une capsule vidéo (disponible à l’adresse monurl.ca/capsulerondelles) à des fins d’enseignement à distance. Cette capsule vidéo présente les étapes clés ainsi que les verbalisations qui peuvent être adaptées pour piloter une telle situation avec des élèves. De plus, un résumé des informations concernant la situation des rondelles se trouve à l’adresse monurl.ca/situationrondelles.

Si vous avez des idées probabilistes à partager à la communauté, n’hésitez pas à le faire sur le groupe Facebook « Pour l’amour de l’enseignement des probabilités ! » (http://www.facebook.com/groups/amourprobs/). Plusieurs ressources qui ont été partagées dans ce groupe ont été répertoriées et organisées sur un site (https://sites.google.com/view/ressources-prob) dont des tâches, articles, capsules vidéos et outils technologiques qui sont accessibles à toute personne intéressée à l’enseignement-apprentissage des probabilités.

Références

  • BATANERO, C., CONTRERAS, J. M., FERNANDES, J. A. et OJEDA, M. M. (2010). Paradoxical games as a didactic tool to train teachers in probability. Dans C. Reading (dir.), Data and context in statistics education: Towards an evidence-based society: Proceeding of the Eighth International Conference on Teaching Statistics (ICOTS8), juillet 2010, Ljubljana, Slovenia. Voorburg, Pays bas : Institut national de la statistique. https://www.stat.auckland.ac.nz/~iase/publications/icots8/ICOTS8_C105_BATANERO.pdf
  • CHERNOFF, E. J. (2019). L’espace échantillonnal : un univers d’interprétations possibles. Dans V. Martin, M. Thibault et L. Theis (dir.), Enseigner les premiers concepts de probabilités : un monde de possibilités ! (p. 195-217). Québec : Presses de l’Université du Québec.
  • THIBAULT, M. (2019a). Des prédictions de couleurs de rondelles… pas si aléatoires que cela ! Dans M.-A. Girard (dir.), Applications pédagogiques des compétences du 21e siècle à l’école secondaire (p. 31-44). Repentigny : Les Éditions Reynald Goulet Inc.
  • THIBAULT, M. (2019 b). Le recours à des simulateurs pour l’enseignement des probabilités. Dans V. Martin, M. Thibault et L. Theis (dir.), Enseigner les premiers concepts de probabilités : un monde de possibilités ! (p. 169-191). Québec : Presses de l’Université du Québec.
  • THIBAULT, M. (2021). Recherche-formation sur l’enseignement des probabilités du secondaire avec des outils technologiques : enjeux de formation. Thèse de doctorat. Université du Québec à Montréal. https://www.researchgate.net/publication/356145559
  • THIBAULT, M. (2023a). Récit #1 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Monty Hall. Envol, 181, 30-35. https://www.researchgate.net/publication/370320198
  • THIBAULT, M. (2023 b). Récit #2 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Jeu de dés. Envol, 182, 6–11. https://www.researchgate.net/publication/374951685
  • THIBAULT, M. (2024). Récit #3 d’une recherche-formation à l’enseignement des probabilités avec des outils technologiques : Bouteille probabiliste. Envol, 183, 12–19. https://www.researchgate.net/publication/380167138
  • VENANT, F. et THIBAULT, M. (2019). Programmer pour apprendre en probabilités. Dans V. Martin, M. Thibault et L. Theis (dir.), Enseigner les premiers concepts de probabilités : un monde de possibilités ! (p. 271-297). Québec : Presses de l’Université du Québec.
Partagez

Articles dans ce numéro