Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

Revue Envol

Revue biannuelle qui est écrite par les membres, pour les membres !

S’approprier la forme
canonique autrement…

avec Desmos Classroom

  • 20 minutes de lecture
Picture of Monique Morel

Monique Morel

Mon premier contact avec la forme canonique a eu lieu au début des années 90 alors que j’étais élève au secondaire. La forme canonique m’avait alors été présentée comme la porte d’entrée de toutes les fonctions et j’ai eu la chance d’avoir accès au logiciel Picasso (ancêtre du logiciel Traces) pour visualiser celles-ci. C’est ce contexte qui m’a permis de développer une image mentale très précise des fonctions et une facilité à travailler avec ces dernières.

Lorsque vingt ans plus tard, au début des années 2010, j’ai eu l’opportunité d’enseigner les mathématiques SN, j’étais heureuse de pouvoir enfin enseigner à mon tour la forme canonique. Pendant plus de cinq ans, j’ai utilisé Allô Prof ou Geogebra pour illustrer le rôle des paramètres en mathématique SN4, mais malgré l’accès à une représentation visuelle et tous mes efforts, je sentais que les élèves ne voyaient pas la même chose que moi et considéraient les paramètres comme une notion abstraite.

Puis, un peu avant la pandémie, j’ai découvert Desmos. C’était l’outil qui me manquait pour transmettre ma propre compréhension des paramètres. Avec Desmos Classroom, j’ai donc créé et fait vivre à mes élèves une séquence d’activités centrée autour d’une fonction non conventionnelle qui leur permet de s’approprier visuellement chaque paramètre de la forme canonique. L’utilisation de cette séquence a fait une grande différence au niveau de la compréhension de mes élèves et de ceux de collègues qui l’ont aussi expérimentée dans leur classe.

Dans cet article, j’expliquerai d’abord le choix de fonction que j’ai fait pour initier les élèves à la forme canonique, ensuite je mettrai de l’avant les principes pédagogiques qui m’ont guidée pour établir l’ordre de la séquence et finalement je présenterai en détail chacune des activités de la séquence avant de conclure en énonçant les éléments-clés qui contribuent, selon moi, à une compréhension approfondie de la part des élèves.

Chapeau canonique

Tout d’abord, pour pouvoir initier les élèves aux paramètres de la forme canonique, il me fallait une fonction de base.

Au fil des années, ce qui m’apparaissait le plus évident, c’est que les conjectures construites par les élèves à partir de leurs observations étaient souvent biaisées. En effet, pour la majorité des fonctions que l’on présente en SN4, il y a des paramètres dont les effets se confondent, ce qui amène les élèves à faire des liens qui ne sont pas toujours adéquats. Le meilleur exemple de conjecture biaisée est la confusion entre le rôle du paramètre a et du paramètre b, qui est causée par l’effet visuel comparable de ces paramètres pour la fonction quadratique, la fonction racine carrée et la fonction valeur absolue.

Pour contrer ce problème et m’assurer que chaque paramètre ait un effet distinctif sur la fonction, j’ai créé avec la calculatrice Desmos une fonction affine par partie non symétrique dont le domaine est restreint. Comme cette fonction ressemblait à un chapeau, j’ai donné le nom «Chapeau canonique» à la séquence d’apprentissage. C’est donc à partir d’une fonction en forme de chapeau que les élèves s’approprient le rôle de chaque paramètre avant de transférer leurs connaissances aux modèles mathématiques habituels.

Principes pédagogiques pour établir l’ordre de la séquence

Pour amener les élèves à maîtriser le rôle des paramètres de la forme canonique dans les modèles mathématiques, j’ai choisi de séparer leur appropriation en quatre temps.

Dans un premier temps, on fait découvrir aux élèves chacun des paramètres individuellement en leur faisant visualiser les transformations géométriques (étirements, contractions, réflexions et translations) qu’ils font subir à un graphique. Cette étape permet aux élèves d’avoir une compréhension adéquate du rôle de chaque paramètre et elle est particulièrement importante pour le paramètre b, qui reste le paramètre le plus difficile à s’approprier.

Dans un deuxième temps, on amène les élèves à reconnaître toutes les transformations que le chapeau a subi et à les associer aux bons paramètres. Cette étape force l’élève à approfondir sa compréhension des transformations tout en associant chaque transformation au bon paramètre. 

Dans un troisième temps, une fois que la compréhension graphique est acquise, on amène les élèves à découvrir à quel endroit chaque paramètre se trouve dans la règle d’une fonction. La règle de la fonction de base est représentée par c(x) et l’élève en vient rapidement à être capable d’ajouter au bon endroit les paramètres a, b, h et k pour obtenir le graphique souhaité.

Finalement, on invite les élèves à relever le défi de trouver des règles et tracer des graphiques de fonctions (quadratique, racine carrée, valeur absolue, sinusoïdale et rationnelle) en mobilisant leurs apprentissages sur les transformations géométriques appliquées aux graphiques et sur la position des paramètres dans la règle. Cette dernière étape renforce l’idée que la forme canonique est une porte d’entrée pour toutes les fonctions.

Présentation des cinq activités de la séquence

La séquence est partagée en cinq activités Desmos différentes qui ont été conçues pour tenter de tenir compte de la durée d’une période de 75 minutes de cours. Toutes les activités de la séquence sont regroupées dans la collection «Chapeau canonique» disponible sur desmosfr.ca.

Vous constaterez rapidement que toutes les activités de la séquence font en sorte que l’élève doit réussir chaque activité avant d’en démarrer une autre et qu’il reçoit une rétroaction immédiate lui permettant de s’ajuster lorsqu’il ne répond pas adéquatement à une question. Ainsi, chaque élève progresse à son propre rythme et l’enseignant, à l’aide du tableau de bord, peut cibler les élèves qui ont le plus de difficultés pour leur offrir une aide personnalisée.

Étant donné la façon dont sont conçues les activités, j’ai ajouté avec le titre de chaque activité un lien vers celle-ci et je vous invite, si possible, à faire l’activité en même temps que vous lisez l’article. Cela vous permettra de mieux comprendre les explications données tout en vous mettant à la place de l’élève.

Chapeau canonique partie 1 2021

La première activité de la séquence permet de découvrir le rôle des paramètres a et b.

L’élève s’approprie d’abord le paramètre a en trois temps.

Dans un premier temps, il commence par observer l’effet du paramètre sur le graphique et formule ses observations (écran 2) avant qu’on lui présente des animations pour illustrer les différents types de transformations produites par le paramètre (écrans 3 à 5).

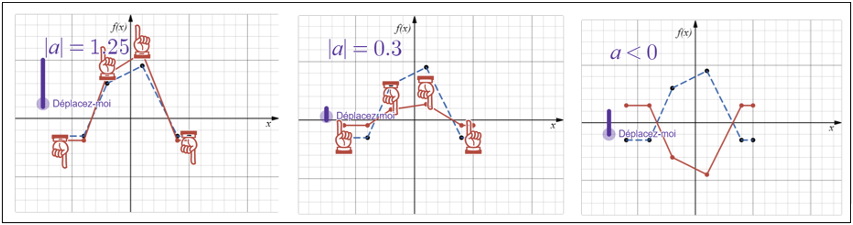
Écrans 3-4-5 de Chapeau canonique 1

Écrans 3-4-5 de Chapeau canonique 1

Dans un deuxième temps, l’élève doit prédire la valeur du paramètre en comparant deux graphiques (écrans 6 à 9). Chaque hypothèse que l’élève fait est illustrée par un graphique vert, ce qui lui permet de rectifier au besoin jusqu’à trouver la bonne valeur. Une fois que l’élève a réussi quatre prédictions, on l’invite à formuler dans ses mots son raisonnement (écran 10) avant qu’il ait accès à une illustration d’une méthode pour trouver la valeur du paramètre cherché (écran 11).

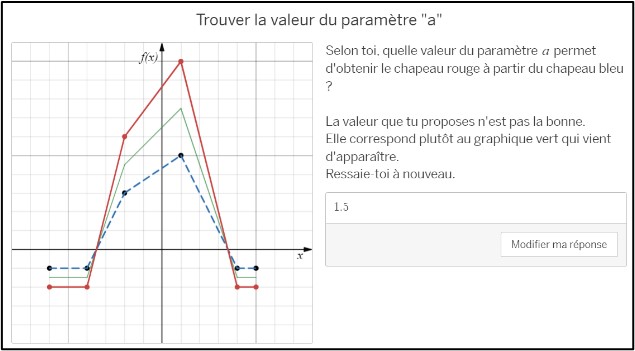
Écran 6 Chapeau canonique 1

Dans un troisième temps, l’élève est invité à transformer un graphique donné à l’aide d’une valeur de paramètre (écrans 12-13). L’animation est construite de telle sorte que l’élève est obligé de déplacer chaque point verticalement, ce qui renforce sa compréhension de l’effet vertical du paramètre a.

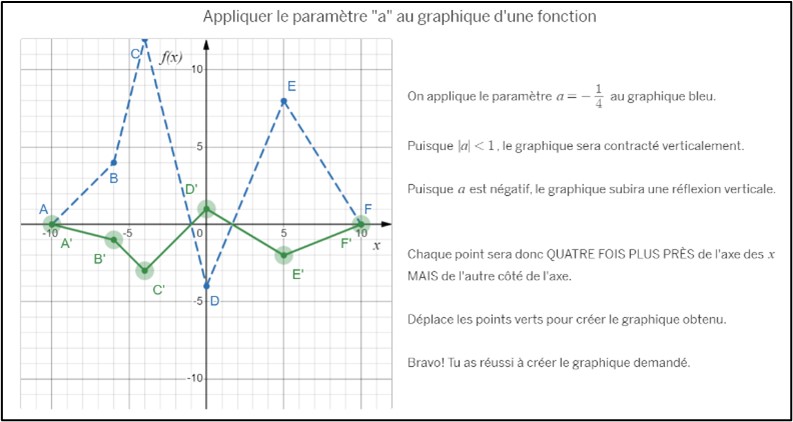Écran 13 Chapeau canonique 1 

Une fois que l’élève s’est approprié le paramètre a, il suit une séquence similaire pour s’approprier le paramètre b (écrans 14 à 25).

Pour terminer l’activité, on propose à l’élève des cartes à associer (écrans 26-27) dans lesquels il doit reconnaître quelle valeur du paramètre a ou du paramètre b correspond à quelle transformation (étirement vertical, étirement horizontal, contraction verticale, contraction horizontale). Ce type d’activité oblige l’élève à prendre conscience des différences et des similitudes entre les deux paramètres.

Écran 26 Chapeau canonique 1

CONSIDÉRATIONS DIDACTIQUES :

L’expérience m’a montré que les élèves suivent des rythmes très différents. Si tous les élèves complètent la découverte du paramètre a durant la période, certains n’arrivent pas à compléter celle du paramètre b et plusieurs n’ont pas le temps de compléter les cartes à associer. Cette différence de rythme se rattrape le cours suivant puisque la deuxième activité est beaucoup plus courte que la première.

Chapeau canonique partie 2 2021

La deuxième activité permet de compléter la découverte du rôle des paramètres avec les paramètres h et k et d’apprendre à reconnaître l’effet de plusieurs paramètres sur un même graphique.

Pour la découverte des paramètres h et k, les activités proposées sont similaires à celles proposées pour la découverte des deux précédents paramètres, soit observer l’effet des paramètres, décrire dans ses mots les observations faites, consulter une animation pour confirmer ses observations, faire des prédictions sur les valeurs des paramètres, formuler dans ses mots son raisonnement pour faire ses prédictions, puis transformer un graphique à partir d’une valeur donnée pour le paramètre.

Maintenant que l’élève s’est approprié les quatre paramètres individuellement, on propose différentes activités pour lui permettre de reconnaître les transformations qui ont été appliquées au graphique d’une fonction et les associer au bon paramètre.

Tout d’abord, on amène l’élève à faire varier les paramètres a et b sur un graphique pour prendre conscience que le seul point du graphique qui n’est pas affecté par ces paramètres est le point qui se situe à l’origine (écran 13). Cette observation est importante pour que l’élève comprenne que les translations ne peuvent pas être observées n’importe où sur le graphique lorsque celui-ci a subi plusieurs transformations.


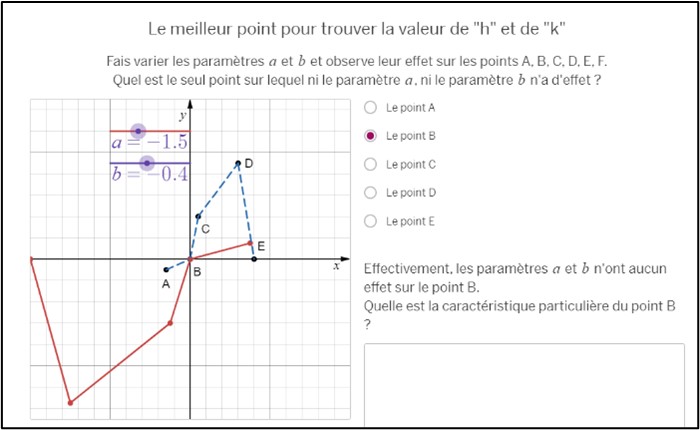
Écran 13 Chapeau canonique 2

Ensuite, on propose une nouvelle activité d’association qui amène l’élève à organiser ses apprentissages de façon à bien associer quelle transformation est produite par quel paramètre (écrans 14 et 15). Cette activité est évidemment plus difficile pour certains élèves, mais c’est une très belle occasion comme enseignant d’engager une conversation avec ces élèves et discuter de leurs erreurs.

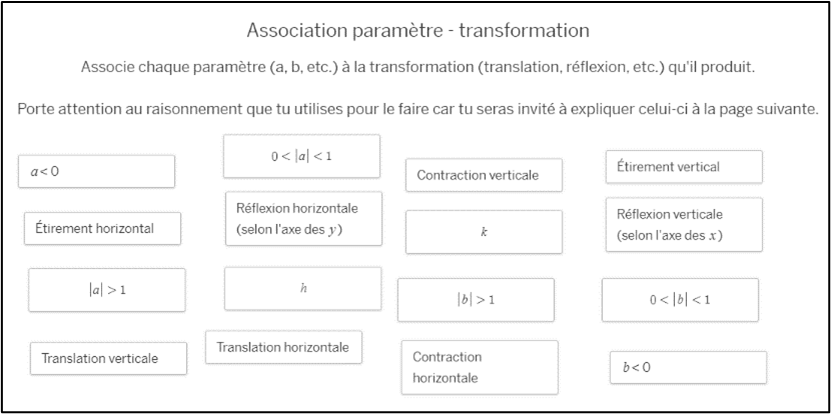
Écran 14 Chapeau canonique 2

Finalement, on présente deux graphiques aux élèves et on leur demande d’identifier quels paramètres ont permis de passer d’un graphique à un autre (écrans 16 à 20). L’objectif ici est de permettre à l’élève de reconnaître les transformations et de les associer au bon paramètre. La valeur du paramètre n’a pas d’importance.

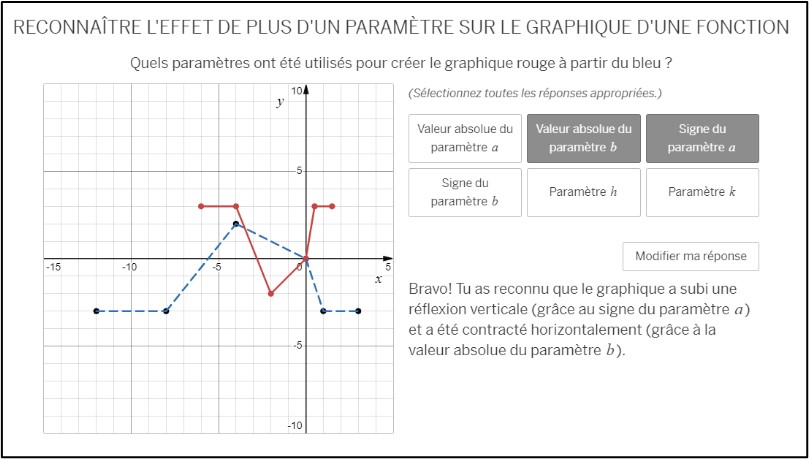
Écran 17 Chapeau canonique 2

CONSIDÉRATIONS DIDACTIQUES: Tel que mentionné à l’activité précédente, cette activité est plus courte que les autres. C’est donc l’occasion de proposer des exercices sur papier aux élèves les plus rapides et d’aider les élèves qui ont plus de difficulté à progresser pour rejoindre le reste du groupe. C’est aussi un bon moment pour faire un retour avec tous les élèves sur les apprentissages faits dans les deux premières activités.

Chapeau canonique partie 3 2021

L’objectif de cette troisième activité est principalement d’approfondir la compréhension du rôle des quatre paramètres sur le graphique d’une fonction. Cela se fait à l’aide de deux types de tâches, soit une où l’élève trouve la valeur des paramètres et une où l’élève transforme un graphique à partir de paramètres donnés.

Pour amener l’élève à trouver la valeur numérique des paramètres impliqués dans la création d’un graphique (écrans 2 à 5), on lui propose un graphique de base, un graphique transformé et un tableau où l’élève peut inscrire les valeurs de paramètres qu’il croit avoir trouvées. À chaque essai, l’élève reçoit des indices pour corriger les paramètres qui n’ont pas été trouvés. De plus, quand l’élève a trouvé les 4 paramètres, on lui présente une animation qui explicite les observations nécessaires pour trouver la valeur de chacun des paramètres.

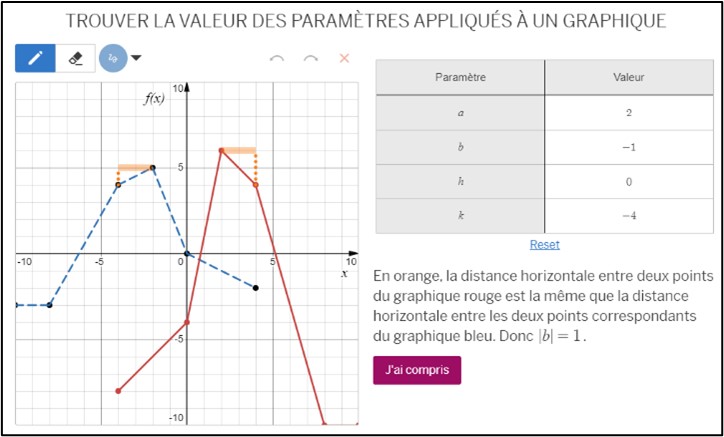
Écran 4 Chapeau canonique 3

La deuxième série de tâches permet à l’élève de transformer adéquatement un graphique à partir des valeurs de plusieurs paramètres. Pour ce faire, on lui propose deux stratégies sous forme de capsule vidéo, soit la méthode graphique axée sur les transformations géométriques (écran 7) qu’il peut pratiquer aux écrans 8 à 10 et la méthode algébrique correspondant à la formule  (écran 11) qu’il peut pratiquer aux écrans 12 à 14. Par expérience, plus les élèves ont une bonne compréhension du rôle des paramètres, plus ils préfèrent la méthode graphique.

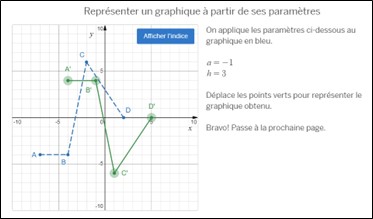
Écran 8 Chapeau canonique 3

CONSIDÉRATIONS DIDACTIQUES: Le niveau de complexité de «Chapeau canonique partie 3 2021» est beaucoup plus grand que dans les deux activités précédentes. Généralement, je place les élèves en équipe de deux pour qu’ils puissent s’entraider. Le fait de vivre cette activité en collaboration favorise la verbalisation, ce qui contribue à augmenter leur compréhension.

Chapeau canonique partie 4 2021

Les trois premières parties de la séquence avaient pour but de développer la compréhension du rôle des paramètres sur le graphique d’une fonction. Maintenant que la compréhension graphique est acquise, la quatrième activité a pour objectif d’initier les élèves à la position des paramètres dans la règle de la fonction.

Pour chacun des paramètres, on présente à l’élève le graphique de deux fonctions avec leur règle et l’élève est invité à identifier le paramètre impliqué en analysant la transformation qui relie les deux graphiques (écrans 2, 4, 6 et 8).

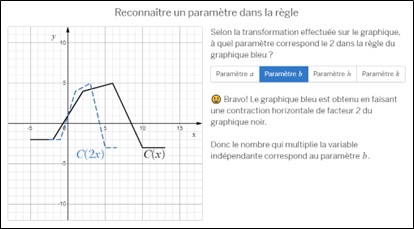
Écran 4 Chapeau canonique 4

On invite ensuite l’élève à trouver la règle associée à un autre graphique qui a été transformé par une autre valeur du même paramètre. S’il se trompe, le graphique correspondant à la règle qu’il a donnée s’affiche et cela permet à l’élève de s’ajuster par lui-même (écrans 3, 5, 7 et 9).

Une fois que l’élève a découvert la position de chaque paramètre dans la règle, on l’invite à trouver la règle d’une fonction dont le graphique a été affecté par deux paramètres (écrans 10 à 13) pour finalement lui présenter la forme canonique de l’équation avec ses quatre paramètres (écran 14).

Écran 14 Chapeau canonique 4

On l’invite ensuite à trouver la règle qui lui permet de tracer un chapeau qui a subi plusieurs transformations (écrans 15 à 19). Il reprend le même type de raisonnement qu’il faisait dans l’activité précédente, mais en plaçant les paramètres au bon endroit dans la règle au lieu de les inscrire dans un tableau.

À la toute fin, on propose une dernière activité (écran 21) où l’élève peut se pratiquer à bien reconnaître la valeur des 4 paramètres dans l’équation en obtenant une rétroaction immédiate.

CONSIDÉRATIONS DIDACTIQUES: Durant cette activité, en tant qu’enseignant.e, il est important de suivre le tableau de bord pour donner de la rétroaction sur la façon d’écrire les règles. En effet, les élèves vont avoir tendance à écrire des 1 et des 0 dans la règle, ce qui est normal à ce stade. Il est important de leur faire voir que les 1 peuvent être sous-entendus pour les paramètres multiplicatifs et que les 0 peuvent être sous-entendus pour les facteurs additifs sans que cela affecte le graphique.

Puissance de la forme canonique

Quatre cours se sont écoulés et on n’a toujours pas abordé les modèles de fonctions. Cela peut paraître beaucoup, mais au cours de ces quatre cours, les élèves ont pu manipuler d’eux-mêmes pour développer une compréhension adéquate de chacun des 4 paramètres. Il ne leur reste plus qu’à transférer ces apprentissages à d’autres modèles de fonctions.

Pour ce faire, les élèves sont invités à relever deux types de défis. Le premier défi (écrans 5 à 12) consiste à trouver la règle associée au graphique d’une fonction à partir de son graphique de base et ce, pour plusieurs modèles de fonctions (quadratique, racine carrée, valeur absolue, rationnelle et sinus). Chaque fois que l’élève donne une règle, le graphique correspondant à sa règle apparaît en vert, ce qui lui permet de valider par lui-même s’il a réussi et rectifier le tir au besoin. Afin d’encourager l’élève à réinvestir ses connaissances et non pas juste procéder par essai-erreur, le nombre de tentatives pour trouver la bonne équation est calculé et affiché à l’écran 14.

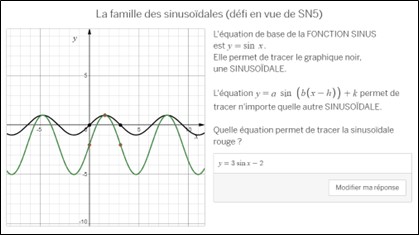
Écran 11 Puissance de la forme canonique

Le deuxième défi (écrans 16 à 20) nécessite de transformer le graphique de base des différents modèles de fonction à partir des paramètres qui se trouvent dans une règle donnée. L’élève reçoit une rétroaction qui lui confirme qu’il a trouvé le bon graphique.

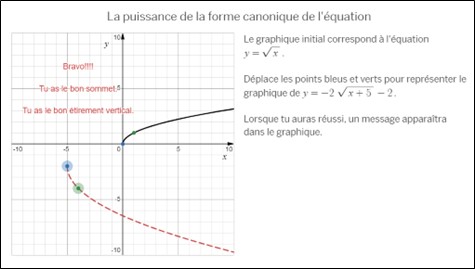
Écran 17 Puissance de la forme canonique

On propose finalement différents exercices d’association de cartes (écrans 25-26-27) pour consolider les apprentissages faits ainsi que des exercices pour tracer des croquis à partir d’une équation canonique (écrans 28-29).

CONSIDÉRATIONS DIDACTIQUES: Tout comme pour l’activité «Chapeau canonique partie 3», il est intéressant de placer les élèves en équipe de deux pour compléter l’activité «Puissance de la forme canonique». En effet, c’est une très belle façon d’inciter les élèves à discuter entre eux de ce qu’ils doivent corriger pour obtenir le bon graphique lorsque leur essai ne fonctionne pas. Il est également préférable de prévoir deux périodes pour cette dernière activité si on veut s’assurer que tous les élèves aient le temps de la terminer en classe.

Conclusion

La séquence d’apprentissage proposée permet aux élèves de faire l’apprentissage en profondeur des paramètres des fonctions. Selon mon expérience et l’expérience d’autres collègues qui l’ont proposée à leurs élèves, il y a trois éléments-clés qui favorisent ce type d’apprentissage.

Le premier élément est sans aucun doute le fait que l’apprentissage se fait sur une fonction non conventionnelle qui permet de vraiment bien différencier le rôle de chaque paramètre. Le deuxième élément est le fait que Desmos renvoie régulièrement à l’élève le résultat de ses essais sous forme de graphique, ce qui provoque immédiatement l’envie et la capacité de se réajuster. Le troisième élément est le fait que l’élève manipule lui-même et à son rythme, ce qui lui donne un meilleur contrôle sur son rythme d’apprentissage.

Vous pouvez accéder à la collection complète ici. Vous pourrez constater qu’il y a aussi dans cette collection l’activité «Comprendre la forme canonique de l’équation» que j’avais créée pour expliquer ce que chaque paramètre fait. J’ai par contre constaté que depuis que je propose cette séquence à mes élèves, le besoin de référer à ces animations a nettement diminué. Je ne l’utilise plus qu’au besoin lorsqu’un élève me questionne. Il y a aussi une autre activité intitulée «Défi canonique» qui a sensiblement le même format que l’activité «La puissance de la forme canonique» et qui génère aléatoirement les valeurs des paramètres, ce qui permet à l’élève qui en ressent le besoin de continuer à se pratiquer à la maison. Vous constaterez aussi qu’il y a des capsules vidéos vers la fin de plusieurs activités. Généralement, j’invite mes élèves à les écouter à la maison pour compléter leurs notes de cours. Il est évidemment possible de masquer ces écrans si vous ne souhaitez pas que les élèves y aient accès.

Pour faire la séquence en entier avec les élèves, il faut prévoir 6 cours. Il est aussi possible d’utiliser seulement certaines parties de la séquence. Par exemple, vous pourriez utiliser seulement les deux premières activités pour faire découvrir les 4 paramètres. Vous pourriez également proposer la dernière activité à vos élèves après avoir enseigné les paramètres de façon plus traditionnelle. Cependant, ayant eu la chance d’expérimenter cette séquence à quelques reprises et d’enseigner en SN5, je peux vous assurer que les périodes consacrées à cette séquence sont très bien investies, tant pour la compréhension de l’élève en SN4 qu’en SN5. D’ailleurs, je vous reviendrai sûrement dans un autre article sur l’utilisation que je fais des paramètres en SN5.

D’ici là, si vous trouvez des coquilles dans les activités, merci de me les signaler à l’adresse monique.morel@csstl.gouv.qc.ca et si vous expérimentez l’activité avec vos élèves, n’hésitez pas à me partager vos impressions.

Partagez

Articles dans ce numéro